Simple Interest – Logical Approach for Quick Solving

<<Prev

Home

Next>>

Terms involved

Before we start solving numericals let us know the terminologies and concepts behind simple interest, in short SI.

Principal/Sum (P): The value of money that is invested for earning interest.

Rate of interest (r): This is the rate at which interest is provided. This is generally given per annum, in short p.a.

Time (t): Duration in years generally. If not, we could make the necessary changes in time.

n month = \displaystyle\frac{n}{12} year

n day = \displaystyle\frac{n}{365} year

\text{SI} = \displaystyle\frac{Ptr}{100} = P\times t\times r\%

Amount (A): A = sum + interest

In simple interest, r is always given on principal, not on amount as in compound interest. So effective or overall interest for t years at r% p.a. is rt% = R% (say)

In that case,

\text{SI}=\text{PR\%}

\text{A}=\text{P(100+R)\%}

Some previous concepts you may find useful while understanding the problems
*Most Important Maths Tricks for Any Exam – Total=100%
**Most Important Maths Tricks for Any Exam – AB Method

Solved Numericals

Q) Find the simple interest on Rs. 7200 at 8% per annum for 10 months
(a) Rs, 480
(b) Rs. 420
(c) Rs. 450
(d) Rs. 410

Ans: (a) Rs, 480

Explanation:

R = 8 \times \displaystyle \frac{10}{12}\% = \displaystyle \frac{20}{3}\%

SI = 7200 \times \displaystyle \frac{20}{300} = 480

Q) The simple interest on a certain sum is Rs. 1560 at the rate of 8% per annum in 2 years. Find the sum
(a) Rs. 9630
(b) Rs. 9140
(c) Rs. 9750
(d) Rs. 9810

Ans: (c) Rs. 9750

Explanation:

16% = 1560

100% = \displaystyle \frac{1560\times 100}{16} = 9750

Q) What sum of money will amount to Rs. 7852 in 4 years at 7 \displaystyle\frac{1}{2}\% per annum simple interest?
(a) Rs. 6010
(b) Rs. 6040
(c) Rs. 6030
(d) Rs. 6070

Ans: (b) Rs. 6040

Explanation:

SI = 4 × 7.5% = 30%

∴ 130% = 7852

⇒ 100% = \displaystyle \frac{7852\times 100}{130} = 6040

Q) Find the amount on a principal of Rs. 3600 for 2 year 9 months at the rate of 8 \displaystyle\frac{1}{3}\% per annum simple interest?
(a) Rs. 57175
(b) Rs. 4425
(c) Rs. 5425
(d) Rs. 4175

Ans: (b) Rs. 4425

Explanation:

t = 2 \displaystyle\frac{9}{12} = \displaystyle\frac{11}{4} yr

r = 8 \displaystyle\frac{1}{3}\% = \displaystyle\frac{25}{3}\%

Rate = \displaystyle\frac{11}{4}\times \displaystyle\frac{25}{3}\%

SI = 3600\times \displaystyle\frac{11 \times 25}{1200} = 825

A = P + SI = 4425

Q) Saksham borrowed certain sum of money at simple interest at the rate of 5% p.a. for the first three years, 9% p.a. for the next five years and 15% for the period beyond 8 years. If the total interest paid by him in 12 years is Rs. 4800, how much money did he borrow?
(a) Rs. 4000
(b) Rs. 2000
(c) Rs. 4500
(d) Rs. 5600

Ans: (a) Rs. 4000

Explanation:

First 3 yrs →5% × 3 = 15%
Next 5 yrs →9% × 5 = 45%
Rest 4 yrs →15% × 4 = 60%

Interest in 12 years = (15 +45 +60)% = 120%

Now, 120% = 4800
⇒ 100% = 4000

Q) Two equal sums of money were invested, one at 4% and other at 4 \displaystyle\frac{1}{2}\%. At the end of 7 years, the simple interest received from the later exceeded that received from the former by Rs. 31.50. each sum was
(a) Rs. 1000
(b) Rs. 500
(c) Rs. 750
(d) Rs. 900

Ans: (d) Rs. 900

Explanation:

Interest difference = (4.5 -4)% × 7 = 3.5%

∴ 3.5% = 35.50

⇒ 100% = \displaystyle\frac{315}{35}\times 100 = 900

Q) Susmita lent some money to Mohit at 5% per annum simple interest. Mohit lent the entire amount to Birju on the same day at 8 \displaystyle\frac{1}{2}\% per annum. In this transaction after a year Mohit earned a profit of Rs. 350. Find the sum of money lent by Susmita to Mohit.
(a) Rs. 10000
(b) Rs. 9000
(c) Rs. 10200
(d) Rs. 18600

Ans: (a) Rs. 10000

Explanation:

Mohit earned a profit of (8.5 – 5 )% = 3.5%

∴ 3.5% = 350
⇒ 100% = 10000

Q) In how many years simple interest obtained on Rs. 8000 at 3% per annum will be equal simple interest on Rs. 6000 at 4% for 5 years?
(a) 4 years
(b) 5 years
(c) 6 years
(d) 8 years

Ans: (b) 5 years

Explanation:

\displaystyle\frac{8000\times 3\times t}{100} = \displaystyle\frac{6000\times 4\times 5}{100}

⇒ t = 5

Aliter:

SI in 2^nd case = 6000 × 20% = 1200

Now, \displaystyle\frac{1200}{8000}\times 100 = 15%

\displaystyle\frac{15\%}{3\%} = 5

Q) In what time will a sum double itself at 8% per annum simple interest?

(a) 12 year

(b) 10 years

(c) 12 \displaystyle\frac{1}{2} year

(d) 10 \displaystyle\frac{1}{2} year

Ans: (c) 12 \displaystyle\frac{1}{2} year

Explanation:

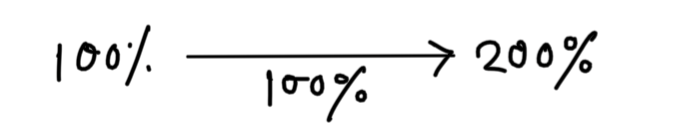
time = \displaystyle\frac{100\%}{8\%} = 12 \displaystyle\frac{1}{2}

---

Basic method:

If principal is P, it has becomes 2P

So, SI = 2P – P = P

Hence, P × t × 8% = P

⇒ t × \displaystyle\frac{8}{100} = 1

⇒ t = \displaystyle\frac{100}{8} = 12 \displaystyle\frac{1}{2}

Q) A certain sum of money triples itself in 5 years at simple interest. In how many years it will be 5 times?
(a) 5 yr
(b) 18 yr
(c) 10 yr
(d) 15 yr

Ans: (c) 10 yr

Explanation:

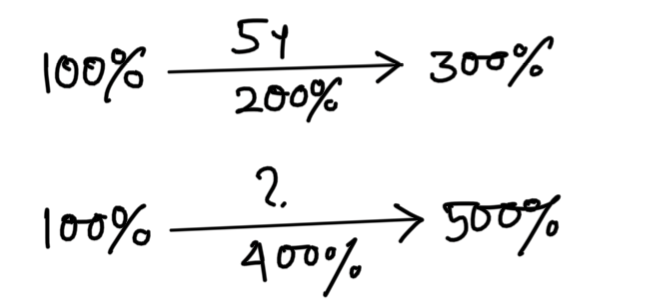
200% = 5 yr

∴ 400% 10 yr

Q) A certain sum of money doubles itself in 9 years at simple interest. In how many years will it become 4 times?
(a) 36 years
(b) 27 years
(c) 18 years
(d) 45 years

Ans: (b) 27 years

Explanation:

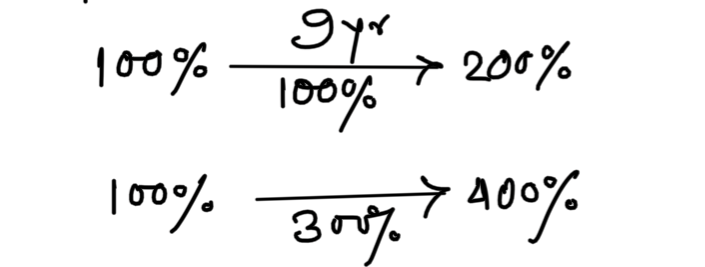
100% = 9 yr

300% = 27 yr

Q) If a certain sum of money becomes thrice of itself in 5 years 4 months at simple interest. What is will be the yearly rate of interest?
(a) 18.75%
(b) 37.5%
(c) 42.25%
(d) None of the above

Ans: (b) 37.5%

Explanation:

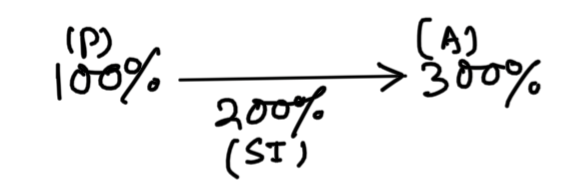
time = 5 year 4 month = 5 \displaystyle\frac{4}{12} = \displaystyle\frac{16}{3} yr

r = \displaystyle\frac{200\%}{\displaystyle\frac{16}{3}} = 37.5%

Q) If a certain sum of money amounts to Rs. 918 in 2 years and Rs. 969 in 3.5 years at simple interest, what is the rate of interest?
(a) 4%
(b) 5%
(c) 6%
(d) 8%

Ans: (a) 4%

Explanation:

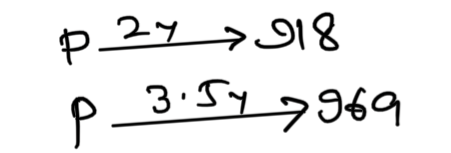
1.5 y = 969 – 918 = 51

∴ 1 y = \displaystyle\frac{51}{1.5} = 34

Si in 2 y = 68

So, P = 918 – 68 = 850

r = \displaystyle\frac{34}{850}\times 100 = 4%

---

Basic Method:

P×(100+2r)% = 918 _____(1)

P×(100+3.5r)% = 969 _____(2)

(2)÷(1) ⟶

\displaystyle\frac{100+3.5r}{100+2r} = \displaystyle\frac{969}{918}

⇒ \displaystyle\frac{1.5r}{100+2r} = \displaystyle\frac{51}{918} [by adding -1 on both side]

⇒ \displaystyle\frac{r}{100+2r} = \displaystyle\frac{51}{918\times 15}\times 10 = \displaystyle\frac{1}{27}

⇒ 27r = 100 +2r

⇒ r = 4

Q) A certain sum amounts to Rs. 7080 in 2 years and Rs. 8430 in 4 \displaystyle\frac{1}{2} year at simple interest. find the rate of interest.
(a) 7%
(b) 8%
(c) 6%
(d) 9%

Ans: (d) 9%

Explanation:

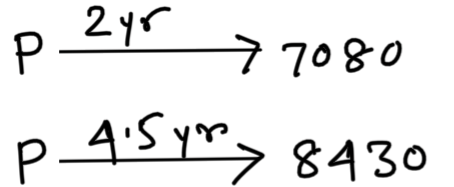
Interest for 2.5 y = 1350

1 y = \displaystyle\frac{1350\times 10}{25} = 540

Principal = 7080 – 1080 = 6000

r = \displaystyle\frac{540}{6000}\times 100 = 9%

Q) A person lent certain sum of money at 5% p.a. SI and in 15 years the interest amounted to Rs. 250 less than the sum lent. What was the sum lent (in Rs.)?
(a) 1000
(b) 1500
(c) 2400
(d) 3000

Ans: (a) 1000

Explanation:

R = 75%

P = 100%

Difference = 25% = 250

∴100% = 1000

Q) A person lent certain sum of money at 9.5% per annum simple interest. In 40 years the interest amounted to Rs. 22400 more than the sum lent. What was the sum lent?
(a) Rs. 8100
(b) Rs. 8500
(c) Rs. 8000
(d) Rs. 8700

Ans: (c) Rs. 8000

Explanation:

P = 100%

R = 40 × 9.5% = 380%

∴ 280% = 22400

⇒ 100% = \displaystyle\frac{22400}{280}\times 100 = 8000

Q) Simple interest on a sum of money will be Rs. 225 after three years. In the next 5 years amount becomes 3 times the principal. What will be the amount in 8 years?
(a) Rs. 1275
(b) Rs. 900
(c) Rs. 1735
(d) Rs. 985

Ans: (b) Rs. 900

Explanation:

SI in 3 years = 225
So, SI/year = 75

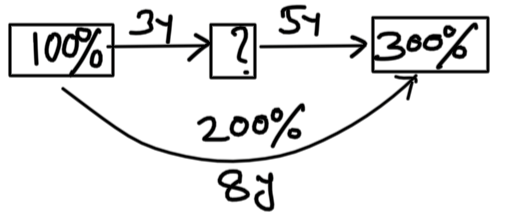
So, 200% = 8 × 75

⇒ 300% = 900

Q) At simple interest Rs. 800 becomes 920 in 3 years. If rate of interest is increased numerically by 3%, the total amount will be
(a) Rs. 972
(b) Rs. 982
(c) Rs. 992
(d) Rs. 1002

Ans: (c) Rs. 992

Explanation:

SI for 3 years = 120

SI/yr = 40

r = \displaystyle\frac{40}{800}\times 100 = 5%

New rate of interest = 8%

So, Amount = P × 124% = 800\times \displaystyle\frac{124}{100} = 992

---

Aliter:

800 amounts to 920 in 3years

Extra interest earned due to extra 3% p.a. interest = 800 × 9% = 72

So, amount = 920 + 72 = 992

Q) A sum of Rs. 400 becomes Rs. 448 at simple interest in 2 years. In how many years will the sum of 550 amounts to 682 at the same rate?
(a) 2 years
(b) 13 years
(c) 3.5 years
(d) 4 years

Ans: (d) 4 years

Explanation:

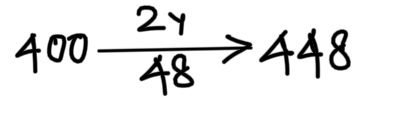
SI/yr = 24

r = \displaystyle\frac{24}{400}\times 100 = 6%

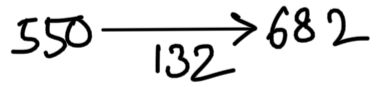
R = \displaystyle\frac{132}{550}\times 100 = 24%

time = \displaystyle\frac{24\%}{6\%} = 4

Q) 2200 rupees become 2464 in 1.5 years at simple interest and the principal amount that will become 9240 in 4 years at the sane rate of interest is
(a) Rs. 9000
(b) Rs. 8000
(c) Rs. 7000
(d) Rs. 5000

Ans: (c) Rs. 7000

Explanation:

SI in 1.5 yr = 464

∴ SI in 1 yr = \displaystyle\frac{464\times 10}{15} = 176

r = \displaystyle\frac{176}{2200}\times 100 = 8%

Now, 132% = 9240

⇒ 100% = \displaystyle\frac{9240}{132}\times 100 = 7000

Q) If a sum of money at simple interest becomes becomes \displaystyle\frac{7}{5} in 4 years, in what time will it become \displaystyle\frac{17}{10} times?
(a) 13 years
(b) 7 years
(c) 14 years
(d) 3.5 years

Ans: (b) 7 years

Explanation:

P = 100, A = 140

r = \displaystyle\frac{40\%}{4} = 10% p.a.

In 2nd case,

P = 100, A = 170

R = 70% overall

So, time = \displaystyle\frac{70\%}{10\%} = 7 years

Q) At a certain rate of simple interest on a sum of money for 10 years, interest will be \displaystyle\frac{3}{5} th of the amount. What is the rate of interest?
(a) 30%
(b) 15%
(c) 10%
(d) 7.5%

Ans: (b) 15%

Explanation:

Let, rate = r% p.a.

R = 10r%

SI = \displaystyle\frac{3}{5} A

⇒ P × 10r% = \displaystyle\frac{3}{5} × P × (100+10r)%

⇒ 50r = 300 + 30r

⇒ 20r = 300

⇒ r = 15

---

Aliter:

SI = \displaystyle\frac{3}{5} A

⇒ \displaystyle\frac{\text{SI}}{\text{A}} = \displaystyle\frac{3}{5}

∴ P = A – SI = 5 – 3 = 2

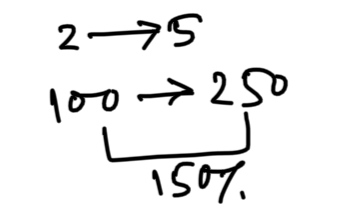
r = \displaystyle\frac{150\%}{10} = 15%

Q) A certain sum was invested on simple interest. The amount to which it had grown in 6 years was \displaystyle\frac{7}{6} times the amount to which it had grown in 4 years. The percentage rate of interest was
(a) 12.5%
(b) 13.5%
(c) 14.5%
(d) 21.5%

Ans: (a) 12.5%

Explanation:

A₆ = \displaystyle\frac{7}{6} A₄

⇒ \displaystyle\frac{\text{A}_6}{\text{A}_4} = \displaystyle\frac{7}{6}

SI in 2 yr = 1 ⇒ 1 yr = \displaystyle\frac{1}{2}

Principal = 6 – 2 = 4

r = \displaystyle\frac{1/2}{4}\times 100 = \displaystyle\frac{1}{8}\times 100 = 12.5%

Q) When a person invests some money under simple interest then at the end of some years the amount become 13 times of the principal and the numerical value of the rate of interest per annum is thrice of the time. At the end of 10 years, the amount will become how many times of the principal at the same rate of interest?
(a) 6 times
(b) 8 times
(c) 9 times
(d) 7 times

Ans: (d) 7 times

Explanation:

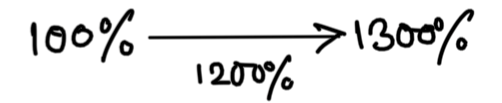
SI = tr%

Let t=x, r=3x%

∴ x × 3x% = 1200%

⇒ 3x² = 1200

⇒ x² = 400

⇒ x = 20

Hence, r = 60%

A₁₀ = 100% + 600% = 700%

Q) A money lender claims to lend money at the rate of 12.5% per annum simple interest. However, he takes the interest in advance when he lends a sum for one year. At what interest rate does he lend the money actually?
(a) 11.14%
(b) 28.14%
(c) 14.28%
(d) 18%

Ans: (c) 14.28%

Explanation:

12.5% = \displaystyle\frac{1}{8} ⇒ Interest of 1 on 8

He takes 1 in advance

So, he is actually giving = 8 – 1 = 7

Hence, actual interest rate = \displaystyle\frac{1}{7}\times 100 = 14.28%

Q) The rate of simple interest per annum of bank being increased from 8.5% to 15% and time duration is reduced from 3.5 years to \displaystyle\frac{13}{5} years. The total simple interest was increased by Rs. 1480. Find the initial simple interest.
(a) Rs. 6047
(b) Rs. 4760
(c) Rs. 7460
(d) Rs. 7640

Ans: (b) Rs. 4760

Explanation:

8.5% × 3.5 = 29.75%

15% × \displaystyle\frac{13}{5} = 39%

Difference = (39 – 29.75)% = 9.25%

∴ 9.25% = 1480

⇒ 29.75% = \displaystyle\frac{1480\times 2975}{925} = 4760

<<Prev

Home

Next>>