How to find unit digit? | Concept of Cyclicity of Number

<<Prev

Home

Next>>

Unit digit is the last digit of any number from right to left. As for example in 123 right most digit is 3, so unit digit is 3. Similarly in 5³ = 125 unit digit is 5. But all the time you cannot expand x^y to a flat number as you easily do in case of 5³ = 125. In this article we are going to discuss how will you find unit digit of xⁿ like 2017²⁰¹⁸ or 144¹⁴⁵ × 126¹²⁶ within seconds.

To solve problems like this we need to invest only some minutes to understand the funda behind it. We just need to have the idea of cyclicity of a number. Cyclicity means when the unit digit( repeats. Didn’t get my point? Don’t worry. Just follow me…

Cyclicity of 0

In 0ⁿ unit digit will be always 0

Cyclicity of 1

In 1ⁿ unit digit will be always 1

Cyclicity of 2

2¹=2
2²=4
2³=8
2⁴=16
2⁵=32
2⁶=64
2⁷=128
2⁸=256
2⁹=…2
2¹⁰=…4
………

Look in 2⁹ and 2¹⁰ we didn’t write the total expansion as we are only concerned with unit digit. Notice that 2, 4, 8, 6 repeats as a unit digit. Total repeating numbers are 4. So we say that cyclicity of 2 is 4. Now to find the unit digit of 2ⁿ we simply divide n by 4 and the remainder will tell about the unit digit.

Q. Find the unit digit number of 2⁵⁴

2^{54} = 2^{(4\times 13)+2}=2^2=4

So unit digit of 2⁵⁴ is 4

Q. Find the unit digit number of 2²²³

2^{223} = 2^{(4\times 55)+3}=2^3=8

So the unit digit number of 2²²³ is 8

Cyclicity of 3

3¹=3
3²=9
3³=27
3⁴=81
3⁵=243
3⁶=…9
3⁷=…7
3⁸=…1
3⁹=…3

Here 3, 9, 7, 1 repeat. So cyclicity is 4

Q. Find the unit digit number of 3²²³

3^{223} = 3^{(4\times 55)+3}=3^3=27=7

So unit digit of 3²²³ is 7

Q. Find the unit digit number of 223²²³

Here I want to mention you one thing that you need to focus only on unit digit of x. If we write the problem in xⁿ form x=223, unit digit=3

223^{223}=3^{223} = 3^{(4\times 55)+3}=3^3=27=7

So unit digit number of 223²²³ is 7.

Note: We can conclude from the above two problems that for power n to various x that have the same unit digit will generate an end number with same unit digit.

Cyclicity of 4

4¹=4
4²=16
4³=64
4⁴=256

Here 4 and 6 are repeating numbers. So Cyclicity is 2. To make it simple we can remember that is unit digit of 4ⁿ is 4 when n is odd number and 6 when n is even number.

Q. Find the unit digit number of 204²²³

n=223→it’s an odd number

So unit digit is 4

Q. Find the unit digit number of 963³⁶⁹ × 204²²³

Just find the unit digit of both the numbers and multiply. Product’s unit digit is required unit digit

963^{369}\times 204^{223}= 3^{369}\times 4^{223}=3\times 4 = 12 =2

So unit digit of 963³⁶⁹ × 204²²³ is 2

Cyclicity of 5

5¹=5
5²=25
5³=125
5⁴=625

Unit digit will be always 5

Cyclicity of 6

6¹=6
6²=36
6³=216
6⁴=…6

So unit digit will be always 6

Cyclicity of 7

7¹=7
7²=49
7³=343
7⁴=…1
7⁵=…7
7⁶=…9
7⁷=…3
7⁸=…1
7⁹=…7

7, 9, 3, 1 repeat. So Cyclicity is 4

Q. Find the unit digit number of 963³⁶⁹ × 204²²³ × 2017²⁰¹

963^{369}\times 204^{223}\times 2017^{201} = 3^{369}\times 4^{223}\times 7^{201}=3\times 4\times 7=84=4

So unit digit of 963³⁶⁹ × 204²²³ × 2017²⁰¹ is 4

Cyclicity of 8

8¹=8
8²=64
8³=512
8⁴=…6
8⁵=…8
8⁶=…4
8⁷=…2
8⁸=…6
8⁹=…8

Here 8, 4, 2, 6 repeat. So Cyclicity is 4

Q. Find the unit digit number of 18¹⁸ × 28²⁸ × 2018²⁰¹⁹

18^{18}\times 28^{28}\times 2018^{2019}
= 8^{18}\times 8^{28}\times 8^{2019}
= 8^{4k_1+2}\times 8^{4k_2+0}\times 8^{4k_3+3} [when 1^st and 3^rd powers are divided by 4, remainders are 2, 3 respectively but 2^nd power is multiple of 4, so we end up in 8⁴ while applying cyclicity]
= 8^{2}\times 8^{4}\times 8^{3}
= 4\times 6\times 2
= 48
= 8

∴ Unit digit is 8

Question. Find the unit digit number of 18^{18}\times 28^{28} \times 2018^{2019}
(a) 8
(b) 4
(c) 2
(d) 6

Ans: (a) 8

Explanation:

18^{18}\times 28^{28}\times 2018^{2019}
= 8^{18}\times 8^{28}\times 8^{2019}

Now, 8^{18}\times 8^{28}\times 8^{2019}
= 8^{4k_1+2}\times 8^{4k_2+0}\times 8^{4k_3+3} [when 1^st and 3^rd powers are divided by 4, remainders are 2, 3 respectively but 2^nd power is multiple of 4, so we end up in 8⁴ while applying cyclicity]
= 8^{2}\times 8^{4}\times 8^{3}
= 4\times 6\times 2
= 48
= 8

So, we have got unit digit = 8

Cyclicity of 9

9¹ = 9
9² = 81
9³ = 729
9⁴ = …1
9⁵ = …9

Hence, when power is odd, unit digit = 9 and when power is even, unit digit = 1

Final Note: You actually don’t require to memorize cyclicity of any number. By practice it will definitely stick to your mind. Anytime you feel doubt just check it, it’s only limited to 4 power max. By following the link provided below practice some problem, so that getting unit digit of a number becomes a piece of cake to you.

Concept of negative remainder to find unit digit

Actually unit digit is the remainder when any number is divided by 10. So, to make a negative remainder positive 10 need to be added with it. See the following example when 29 is divided by 10 to get the unit digit 9.

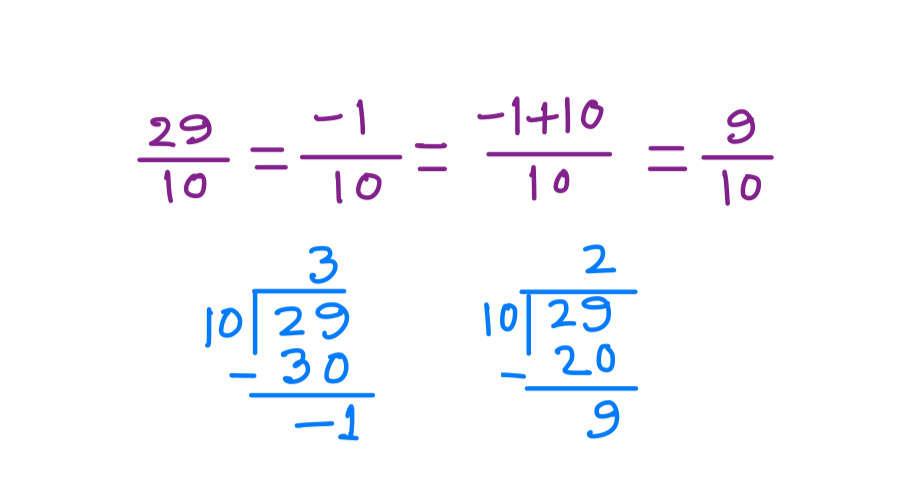
Question: What is the digit in the unit place of 24^{63}+33^{61}-27^{58}

24^{63}+33^{61}-27^{58}\\ =4^{63}+3^{61}-7^{58}\\ =4+3-9\\ =-2\\ =-2+10\\ =8\\

Question: If x=164^{169}+333^{337}-727^{726}, then what is the unit digit of x?

164^{169}+333^{337}-727^{726}\\ =4^{169}+3^{337}-7^{726}\\ =4+3^{1}-7^{2}\\ =4+3-9\\ =-2\\ =-2+10\\ =8\\

<<Prev

Home

Next>>