The income of A is 80% of B’s income and the expenditure of A is 60% of B’s expenditure. If the income of A is equal to 90% of B’s expenditure, then by what percentage are the savings of A more than B’s savings?
(a) 100%
(b) 140%
(c) 125%
(d) 150%
{Previously asked in SSC CGL Mains 2020}

Ans: (b) 140%

Explanation:

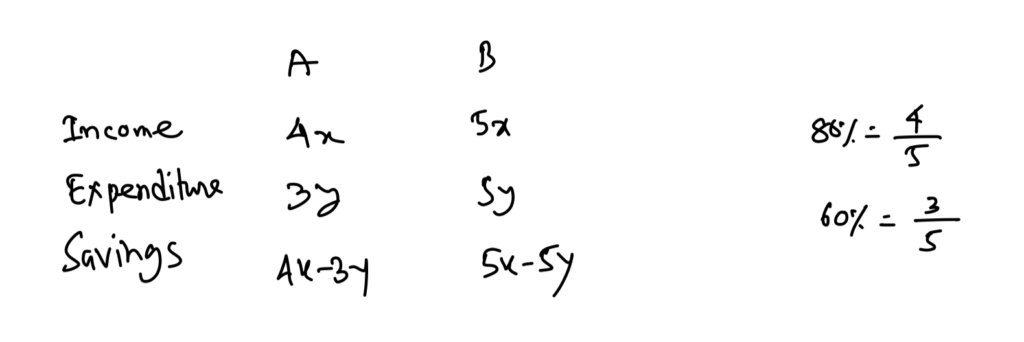
ATQ, Income of A = 90% of B’s Expenditure

\therefore 4x = \displaystyle\frac{9}{10}\times 5y

\Rightarrow \displaystyle\frac{x}{y} = \displaystyle\frac{9}{8}

Let, x = 9
\qquad y=8

Now, Savings of A = 36 – 24 = 12
\qquad Savings of B = 45 – 40 = 5

% more = \displaystyle\frac{7}{5}\times 100 = 140%

Aliter:

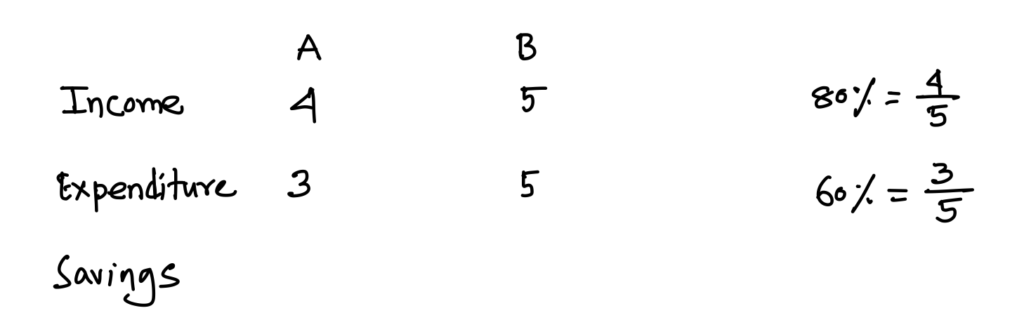
Now, we want to make income of A equal to expenditure of B keeping income and expenditure ratio const.

Actually our target is to make income of A equal to 90% of expenditure of B.

Now, 90% = \displaystyle\frac{9}{10}

This means ratio of A’s income to B’s expenditure will be 9 : 10

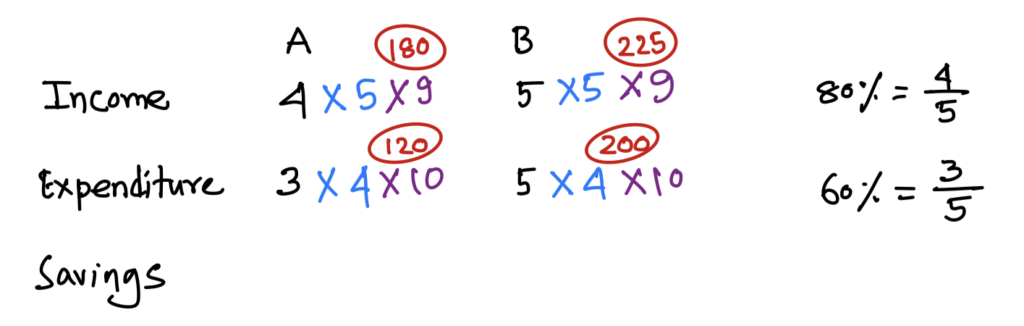
Now, calculate savings from Income = Expenditure + Savings formula

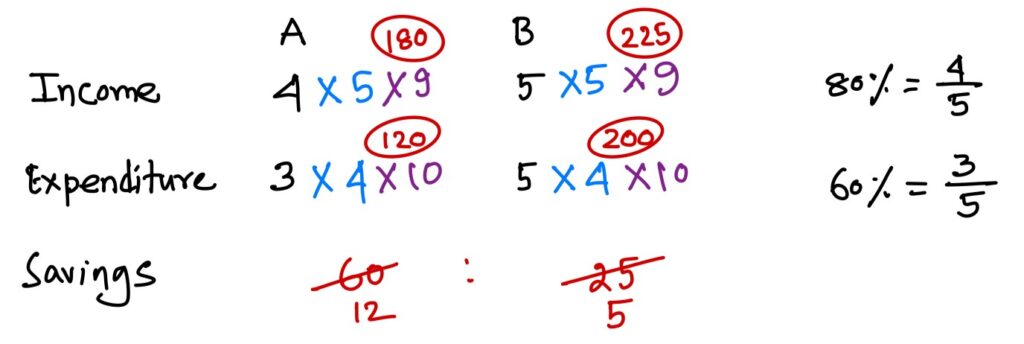
% more savings = \displaystyle\frac{7}{5}\times 100 = 140%