Most Important Maths Tricks for Any Exam

This method has multiple applications. Just keep patience with us while we are trying to make you understand the concepts.

how would you solve the following problem?

A rectangle has length 40 cm, breadth 20 cm. Length is increased by 25% and breadth is increased by 20%. What will the the percent change in area?

Explanation:

Area = 40 × 20 = 800 cm²

New area = (40 + 40 × 0.25) × (20 + 20×0.20)
$\qquad\qquad$ = 50 × 24
$\qquad\qquad$ = 1200 cm²

Increase in area = $\displaystyle \frac{1200-800}{800} \times 100$ = 50%

In shorter way you can find the answer by this way, 25 + 20 + 5 = 50%

How does this extra 5 comes?

This is a term comes from $\displaystyle \frac{25\times20}{100}$ which can be understood from ab method.

Jump ahead to

What is AB Method?

let’s say $a$ and $b$ are percentage change in any problem

Net change, $(a, b)$ ⟶ $\left(a+b+\displaystyle \frac{a\times b}{100}\right)\%$

Increasing term will be “+ve” and decreasing term will be “-ve“

Note: if any problem involves product of more than two terms, equivalent of any two terms will be taken with remaining term. See the following solved problems to understand it.

Let’s resolve the previous problem
Length and breadth both increases

$(25, 20)$ ⟶ $25+20+\displaystyle \frac{25\times 20}{100}$ = $50\%$

Where to use ab method?

This method is useful in the following cases

Change in product when variables are changed
Successive change
Discount
Compound Interest
Dishonest Dealer problems

Application 1 : ab ≠ const. case

\begin{align*} a \times b & = \text{P}\\ a \uparrow \times b\uparrow &= (\text{P}\uparrow?) \\ a \downarrow \times b\downarrow &= (\text{P}\downarrow?) \\ a \uparrow \times b\downarrow &= (\text{P}\uparrow?) \ \text{OR} \ (\text{P}\downarrow?)\\ \end{align*}

Here P stands for product

Question: The radius of a circle is 9.5 cm. If it increases by 10%, by what percent area will increase?

Ans: 21%

Explanation:

Area = $\pi r^2 = \pi \times r \times r$

here both a = 10 and b = 10

$(10, 10)$ ⟶ $10+10+\displaystyle\frac{10\times 10}{100}$ = 21%

Problems on concept: price × consumption = expenditure

Question: The price of petrol increases by 20% and therefore a motor rider decreases his consumption by 10%, by what percent expenditure changes?

Ans: Expenditure will increase by 8%

Explanation:

(20, -10) ⟶ 20 – 10 -2 = 8%

Question: The price of petrol increases by 20%, by what percent a motor rider must decrease his consumption so that net expenditure can go up by 8% only?

Ans: 10%
Explanation:

Let the decease is $x\%$

\begin{align*} & (20,-x) \rightarrow 8\% \\ & \therefore 20-x+\frac{20 \times -x}{100} =8 \\ & \Rightarrow 20-x-\frac{1}{5} x =8 \\ & \Rightarrow 20-\frac{6}{5} x =8 \\ & \Rightarrow \frac{6}{5} x =12 \\ & \Rightarrow x =10 \\ \end{align*}

Similar Problem: The price of sugar is reduced by 25% but in spite of the decrease, Aayush ends up increasing his expenditure on sugar by 20%. What is the percentage change in his monthly consumption of sugar? [Ans: 60% increase]

What if a problem involves product like a × b × c × ….

If any problem involves product of more than two terms, equivalent of any two terms will be taken with remaining term. See the following solved problems to understand it.

Question: The radius of a sphere is 9.4 cm. If it is increased by 10% by what percent will its volume increase?

Ans: 33.1%

Explanation:

Volume = $\displaystyle \frac{4}{3}\pi r^3$ = $\displaystyle \frac{4}{3}\pi \times r \times r \times r$

\begin{align*} (10, 10) &\rightarrow 10+10+\frac{10\times 10}{100} \\ &=21\% \\ \end{align*}

\begin{align*} (21, 10) &\rightarrow 21+10+\frac{21\times 10}{100} \\ &=31+2.1 \\ &=33.1\% \\ \end{align*}

Question: The radius of a sphere is decreased by 10% by what percent will its volume decrease?

Ans: 27.1%

Explanation:

Volume = $\displaystyle \frac{4}{3}\pi r^3$ = $\displaystyle \frac{4}{3}\pi \times r \times r \times r$

\begin{align*} (-10, -10) & \rightarrow -10-10+\frac{-10\times -10}{100} \\ &=-20+1 \\ &=-19\% \\ \end{align*}

\begin{align*} (-19, -10) & \rightarrow -19-10+\frac{-19\times -10}{100} \\ &=-29+1.9 \\ &=-27.1\% \\ \end{align*}

Question: The length , breadth and height of a cuboid are increased by 30%, 20% and 10% respectively, by what percent will the volume of cuboid increase?

Ans: 71.6%

Explanation:

Volume of cuboid = length × breadth × height

(30, 20) ⟶ 30 + 20 + 6 = 56%

(56, 10) ⟶ 66 + 5.6 = 71.6%

Question: The radius of a cylinder increases by 20% and its height increases by 10%, by what percent will its volume increase?

Ans: 58.4%

Explanation:

Volume of cylinder = πr²h = π × r × r × h

Here, r = radius = 20% and h = height = 10%

(20, 20) ⟶ 40 +4 = 44%

(44, 10) ⟶ 54 + 4.4 = 58.4%

HW1: The radius of a cylinder increases by 20% and its height decreases by 10%, by what percent will its volume increase or decrease? [Try answering in comment]

Application 2 : Successive Change

Question: A sales an article to B at profit of 10%. B sales it to C at a profit of 20%. C’s price is what percent more than A’s price?

Ans: 32%

Explanation:

(10, 20) ⟶ 10 + 20 + 2 = 32%

By Traditional Method

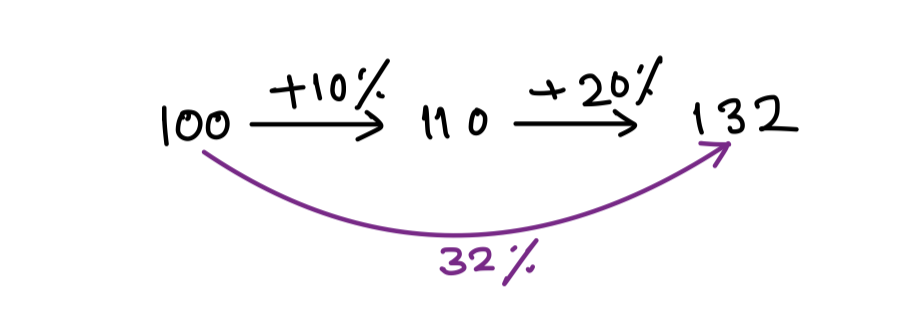
Question: Two successive discount of 20% and 10% is equivalent to single discount to what percent?

Ans: 28%

Explanation:

(-20, -10) ⟶ – 20 – 10 + 2 = – 28%

Question: Three successive discount of 15%, 20% and 10% are equivalent to what single discount?

Ans: 38.8%

Explanation:

(-15, -20) ⟶ – 35 + 3 = – 32%

(-32, -10) ⟶ – 42 + 3.2 = – 38.8%

Question: Twenty successive discount of 5%, 10%, 15%, 20%, … is equivalent to what single discount?

Ans: 100%

Explanation:

5, 10, 15 are AP series (Arithmetic Progression) with difference 5

So 20th term = 5 + 19 × 5 = 100

The last discount is automatically 100%. Actually we don’t even require to use ab method here.

Another way to find 20th term:
1st term 5 = 5 × 1
2nd term 10 = 5 × 2
3rd term 15 = 5 × 3
⁞
20the term = 5 × 20 = 100

[Not Part of the problem] Just for curiosity if you want to see what happen if we apply ab method see the following calculation I have done in excel

Application 3 : Discount

People like discount. The seller is intelligent. So, he marks products at certain percentage higher on cost price. Then sells the product after giving some discount on marked price to have overall profit on cost price.

This is also successive change

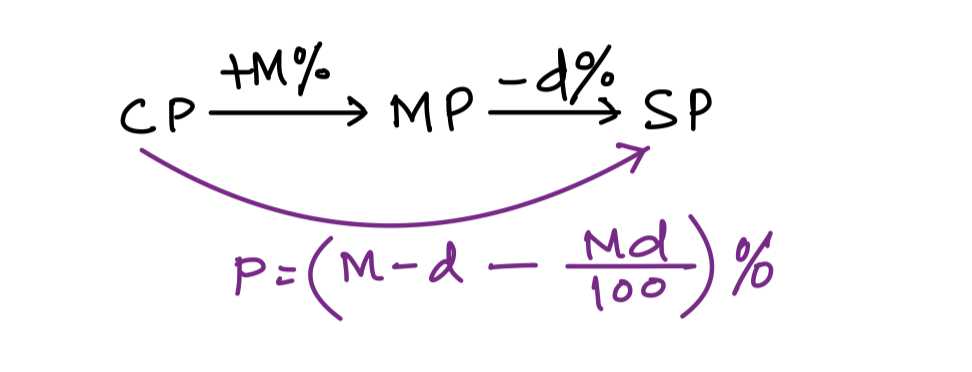
Don’t try to remember the formula. Just try to understand a and b of ab method with sign and answer will be ready. See the following examples.

Question: A man marks his goods 40% above the CP and gives a discount of 10%. What percent profit does he make?

Ans: 26%

Explanation:

(40, -10) $\rightarrow$ 40 – 10 + $\displaystyle \frac{40\times -10}{100}$ = 30 – 4 = 26

Question: What percent above should a dealer marks his goods so that after giving a discount of 20%, he will get 20%?

(x, -20) $\rightarrow$ 20

⇒ x – 20 – $\displaystyle\frac{20x}{100}$ = 20

⇒ $\displaystyle\frac{4}{5}$ x = 40

⇒ x = 50

Application 4 : Compound Interest

Effective single interest for compound interest can be calculated using ab method. Some of the most asked interest rate is calculated for your ready reference. If possible remember effective single interest for three years for 4%, 5%, 10% and 20%. If you forget or in confusion just calculate the value using ab method

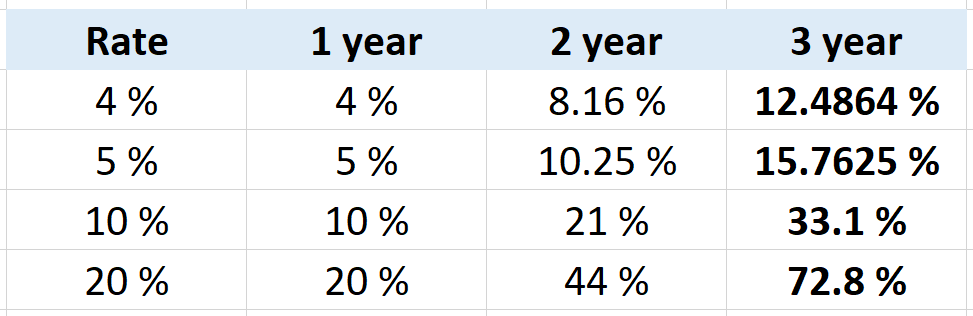
Question: The difference between simple interest and compound interest on a certain sum of money for 2 years at 5% per annum is ₹10. Find the sum.
(a) ₹4600
(b) ₹4800
(c) ₹4500
(d) None of these

Ans: (d) None of these

Explanation:

Equivalent interest for 2 years
In CI, (5, 5) ⟶ 10.25%
In SI, 2 ×5% ⟶ 10%

Interest rate difference = 10.25% – 10% = 0.25%

∴ 0.25% = 10
100% = 4000

So, the sum is ₹4000

Question: What will be the difference between simple interest and compound interest at 4% per annum on a sum of ₹5000 after 3 years?
(a) ₹24.32
(b) ₹28.56
(c) ₹32.48
(d) ₹36.18

Ans: (a) ₹24.32

Explanation:

(4, 4) ⟶ 8 + 0.16 = 8.16%

(8.16, 4) ⟶ 12.16 + 0.3264 = 12.4864%

Rate Difference = 12.4864% – 12% = 0.8468%

So, interest difference = 5000 × 0.8468% = 24.32

Application 5 : Dishonest Dealer

Question: A dishonest shopkeeper sells sugar at Rs. 18/kg which he has bought at Rs. 15/kg and he is giving 800 gm instead of 1000 gm. Find his actual profit percentage.

Ans: 50%

Explanation:

If we apply ab method for monetary gain and weight gain, we would get the net profit.

For the given problem,

CP = 15, SP = 18

\begin{align*} \text{Monetary gain} &= \frac{\text{P}}{\text{CP}}\times 100 \\ &= \frac{3}{15}\times 100\\ &=20\%\\ \end{align*}

\begin{align*} \text{Weight gain} &= \frac{\text{Error}}{\text{Faulty weight}}\times 100 \\ &= \frac{1000-8000}{800}\times 100\\ &=\frac{200}{800}\times 100\\ &=25\%\\ \end{align*}

Now applying ab method,
(20, 25) ⟶ 20 + 25 + $\displaystyle\frac{20\times 25}{100}$ = 50%

So, actual profit = 50%.

We have a fully dedicated post on dishonest dealer and faulty weight. You may check that for more problems on part

Most Important Maths Tricks for Any Exam – AB Method

What is AB Method?