Most Important Maths Tricks for Any Exam : Total = 100%

<<Prev

Home

Next>>

Apart from some basic maths tricks, we will try to make you aware some of the most important maths tricks for any competitive exams. Just focus on how the concepts work rather than the fancy name of the method. Just joking! Remember the name of the method and how it works so that it can help you and your kids too!

While we would try to explain the concepts just keep patience and go on.

Try solving this:

In an exam one student get 25% marks and fails by 30 marks. Another student get 40% which is 60 more than the passing mark. Find full marks in the exam?

Generally we would solve like this.
Let total marks = x

So, pass marks = \displaystyle {\frac{25}{100}x+30} = \displaystyle \frac{40}{100}x-60

On solving, x = 600

Hence full marks = 600.

But this can be solved in more time efficient way. See below….
15% = 90
⇒ 100% = 600
Hence full marks = 600.

Wonder how this work! Keep going.

How to use Total = 100% ?

1. Read the question and find out what % equals to what actual number that can be interpreted from the question
2. Find the required% using unitary method with the help of interpreted value.

Question: In an exam one student get 25% marks and fails by 30 marks. Another student get 40% which is 60 more than the passing mark. Find full marks in the exam?
(a) 150
(b) 180
(c) 600
(d) None of these

Ans: (c) 600

Explanation:

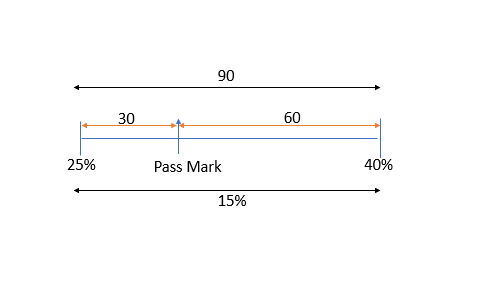
Percentage marks difference = 40% – 25% = 15%
Marks difference = 60 + 30 = 90 (Since one’s marks less than passing marks and another’s is more than passing marks)
∴ 15% = 90
⇒ 100% = 600
Hence full marks = 600.

Where to use Total = 100% ?

This method can be applicable to

• Percentage Problems
• Profit and Loss Problems
• Simple Interest Problems

Application on Percentage

Here, base of calculation = 100%

Question: In a class 70% students are present and 90 students are absent. Find total number of students?

Ans: 300

Explanation:

30% students are absent
∴ 30% = 90
⇒ 100% = 300

Question: In an election contest between 2 candidates one get 60% vote and wins by a majority of 400 votes. Find the total number of votes?

Ans: 2000

Explanation:

Votes by winner = 60%
and votes by loser = 40%
Difference = 60% – 40% = 20%

∴ 20% = 400
⇒ 100% = 2000

Question: In an exam one student get 25% marks and fails by 30 marks. Another student get 40% which is 60 more than the passing mark. Find the passing percentage?

Ans: 30%

Explanation:

Passing marks = (25% + 30) OR (40% – 60)

15% = 90
⇒ 25% = 150
⇒ 100% = 600

Hence passing marks = 150 + 30 = 180

Pass percentage = \displaystyle \frac{180}{600}\times 100 = 30\%

Application on Profit and Loss

Here base of calculation, CP = 100%

Question: A man sales an article at a loss of 10%, if he had sold the article at ₹30 more, he could have got a profit 5%. find his cost price?

Ans: 200

Explanation:

15% = 30
⇒ 100% = 200

Question: A man sells an article at ₹230 and gains 15%. Find the cost price of the article?

Ans: ₹200

Explanation:

Selling price is 115% of CP since profit is 15%

∴ 115% = 230
⇒ 100% = 200

Question: By selling an article at ₹270 a man losses 10%. At what price should he sell it so as to get 20%?

Ans: ₹360

Explanation:

∴ 90% = 270
⇒ 120% = 360

Application on Simple Interest

Here base of calculation, Principal = 100%

Question: A  sum of money deposit in a bank  for a period of 4 year at 8.5% p.a simple interest earns an interest of Rs 850. Find the sum.

We know, simple interest is equal for every year.

Rate = 4 × 8.5% = 34%

∴ 34% = 850

⇒ 100% = \displaystyle\frac{850\times 100}{34} = 2500

Question: A man deposits a certain amount in a bank at 7% per annum simple interest. If he had deposited the same money in a post office, he could get 8.5% per annum and in that case he would have received ₹300 more. How much money had he deposited in the bank?

Ans: ₹20000

Explanation:

∴ 1.5% = 300
⇒ 100% = 20000

Question: Susmita lent some money to Mohit at 5% per annum simple interest. Mohit lent the entire amount to Birju on the same day at 8 \displaystyle\frac{1}{2}\% per annum. In this transaction after a year Mohit earned a profit of Rs. 350. Find the sum of money lent by Susmita to Mohit.

Ans: Rs. 10000

Explanation:

Mohit earned a profit of (8.5 – 5 )% = 3.5%
∴ 3.5% = 350
⇒ 100% = 10000

Question: Two equal sums of money were invested, one at 4% and other at 4 \displaystyle\frac{1}{2}\%. At the end of 7 years, the simple interest received from the later exceeded that received from the former by Rs. 31.50. Each sum was

Ans: Rs. 900

Explanation:

For simple interest interest rate is same for every year. Here we have to find difference for 7 years.

Interest difference = (4.5 -4)% × 7 = 3.5%

∴ 3.5% = 31.50

⇒ 100% = \displaystyle\frac{315}{35}\times 100 = 900

You may check out our simple interest problems post also.

Other Post You may like:
*Most important maths tricks for any exam – AB Method
**Most important maths tricks for any exam – Line Method

<<Prev

Home

Next>>