Previous Year Average Questions For SSC CGL Mains/Tier II till date

In this post, you will find average questions from SSC CGL Mains from 2013 to the latest Mains exam. In this post, we may not be discussing multiple methods for single problems but the concept post will be linked for referral wherever possible.

By the way, if you want to refer to the concept building post first, visit
1. Average Basics
2. Average of AP Series
3. Average Advanced Problems

Jump ahead to

SSC CGL MAINS 2020

Q1. In an examination, average marks of a student per paper were 71. If he would have obtained 35 more marks in science, 11 more marks in history and 4 more marks in computer science, his average marks per paper would have been 76. How many papers were there in the examination?
(a) 15
(b) 12
(c) 18
(d) 10
{Held on: Jan 29, 2022}

Ans: (d) 10

Explanation:

Extra Marks = 35 + 11 +4 = 50
For this marks average is increased by (76 – 71) = 5
If no of subject = x

$\displaystyle\frac{50}{\text{x}}$ = 5 ⇒ x = 10

Q2. The numbers of students in section A and section B of a class are 50 and 62 respectively. The average score in mathematics of all the students is 75. If the average score of the students in section A is 20% more than that of students in section B, then what is the average score of students in section A (correct to one decimal place)?
(a) 84.3
(b) 82.6
(c) 87.5
(d) 85.7
{Held on: Jan 29, 2022}

Ans: (b) 82.6

Explanation:

Ratio of numbers of students in section A to that of section B
= 50 : 62
= 25 : 31

$20\%=\displaystyle\frac{1}{5}$ ⇒ 1 more on 5

Let, avg score of section B = 5x
then avg score of section A = 6x

We have to find out 6x = ?

25 × 6x + 31 × 5x = (25 + 31) × 75

⇒ 30x + 31x = 56 × 15 [By dividing both side by 5]

⇒ 61x = 56 × 15

⇒ 6x = $\displaystyle\frac{56\times 15\times 6}{61}$ = $\displaystyle\frac{56\times 90}{61}$ = $\displaystyle\frac{5040}{61}$ = 82.6

Q3. The average of n numbers is 45. If 60% of the numbers are increased by 5 each and the remaining numbers are decreased by 10 each, then what is the average of the numbers so obtained?
(a) 42
(b) 43
(c) 46
(d) 44
{Held on: Feb 3, 2022}

Ans: (d) 44

Explanation:

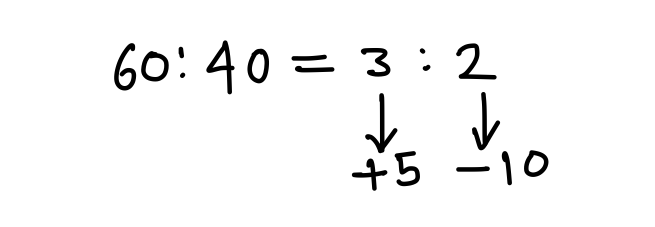
Net change in avg = $\displaystyle\frac{+15-20}{5}$ = $\displaystyle\frac{-5}{5}$ = $-1$

New avg = 45 – 1 = 44

Q4. The number of students in a class is 45, out of which $33\displaystyle\frac{1}{3}\%$ are boys and the rest are girls. The average score of girls in Science is $66\displaystyle\frac{2}{3}\%$ more than that of boys. If the average score of all the students is 78, then the average score of girls is:
(a) 78
(b) 54
(c) 90
(d) 68
{Held on: Feb 3, 2022}

Ans: (c) 90

Explanation:

$33\displaystyle\frac{1}{3}\% =\displaystyle\frac{1}{3}$ ⇒ 1 is boys on every 3 students

B : G = 1 : 2

$66\displaystyle\frac{2}{3}\% = \displaystyle\frac{2}{3}$ ⇒ 2 is more on 3

Let, Avg score of boys = 3x
So, Avg score of girls = 5x

We have to find out 5x = ?

Now,

\begin{align*} & 1\times 3x + 2 \times 5x = 3\times 78 \\ & ⇒ 13x = 3\times 78 \\ & ⇒ x = 18 \\ & ⇒ 5x = 90\\ \end{align*}

Q5. The average of 25 numbers is 64. The averages of the first 13 numbers and that of the last 13 numbers are 62.8 and 72.2, respectively. If the 12th number is 61, and if the 12^th and 13^th numbers are excluded, then what is the average of the remaining numbers (correct to one decimal place)?
(a) 70
(b) 60.2
(c) 71
(d) 60
{Held on: Feb 3, 2022}

Ans: (b) 60.2

Explanation:

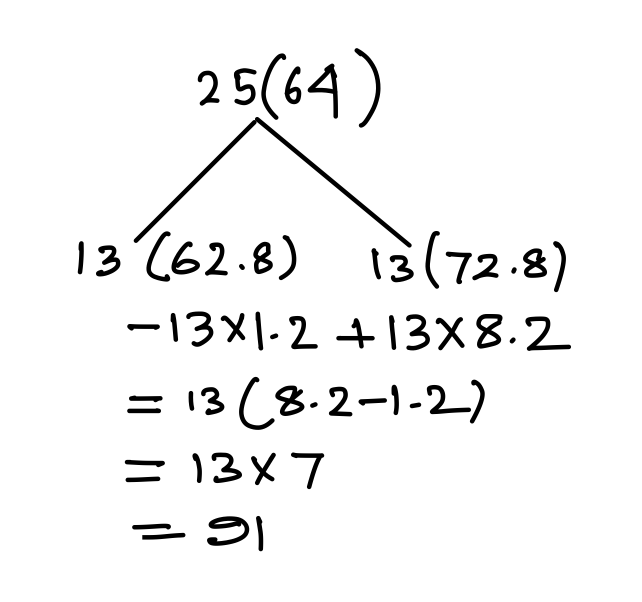
13^th No = 64 + 91 = 155

Now, we have to find out average of 23 No excluding 12^th and 13^th

\begin{align*} \text{Required Avg} &= \frac{25\times 64-61-155}{23}\\ &=\frac{1600-216}{23}\\ &=\frac{1384}{23}\\ &=60.2\\ \end{align*}

SSC CGL MAINS 2019

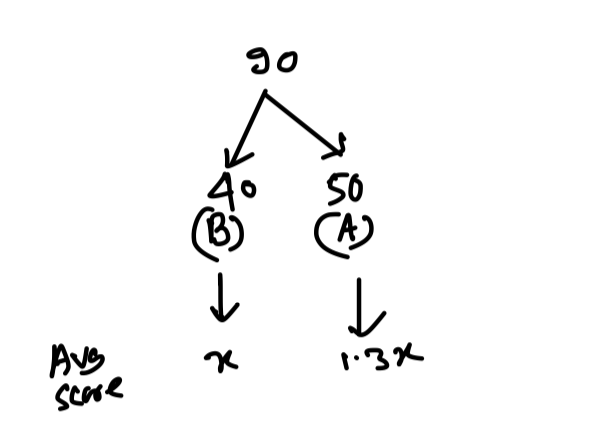
Q1. The average score in Mathematics of 90 students of sections A and B of class IX was 63. The number of students in A were 10 more than those in B. The average score of students in A was 30% more than that of students in B. The average score of students in B is:
(a) 60
(b) 54
(c) 50
(d) 56
{Held on: Nov 15, 2020}

Ans: (b) 54

Explanation:

90 = 40 + 50

Ratio of no of students in section A to that of section B
= 50 : 40
= 5 : 4

$30\% = \displaystyle\frac{30}{100} = \displaystyle\frac{3}{10}$ ⇒ 3 is more on 10

∴ Avg score of students of Section A = 13x
and Avg score of Section B = 10x

We have to find out 10x = ?

Now,

\begin{align*} & 4\times 10x + 5 \times 13x = 9\times 63\\ & ⇒40x + 65x = 9\times 63\\ & ⇒ 105x = 9\times 63\\ & ⇒ 10x = \frac{9\times 63\times 10}{105} = 54\\ \end{align*}

Aliter(By Traditional Method)

Given data in this question are quite simple unlike Q2 of 2020. So basic method will may give answer more quickly.

\begin{align*} & 40x + 50 \times 1.3x = 90\times 63\\ & ⇒40x + 65x = 90\times 63\\ & ⇒ 105x = 90\times 63\\ & ⇒ 10x = \frac{90\times 63}{105} = 54\\ \end{align*}

Q2: The average of three numbers a, b and c is 2 more than c. The average of a and b is 48. If d is 10 less than c, then average of c and d is:
(a) 36
(b) 40
(c) 35
(d) 38
{Held on: Nov 15, 2020}

Ans: (b) 40

Explanation:

a + b + c = 3(c + 2)
⇒ a + b = 2c + 6

a + b = 2 × 48 = 96

∴ 2c + 6 = 96
⇒ c = 45

So, d = 45 – 10 = 35

Hence, $\displaystyle\frac{\text{c}+\text{d}}{2}$ = $\displaystyle\frac{45+35}{2}$ = 40

Q3. The average of twenty-five numbers is 54. The average of the first 13 numbers and that of the last 13 numbers is 52.8 and 62.2, respectively. If the 13th number is excluded, then what is the average of the remaining numbers (correct to one decimal place)?
(a) 51.2
(b) 49.8
(c) 50.2
(d) 50.6
{Held on: Nov 15, 2020}

Ans: (c) 50.2

Explanation:

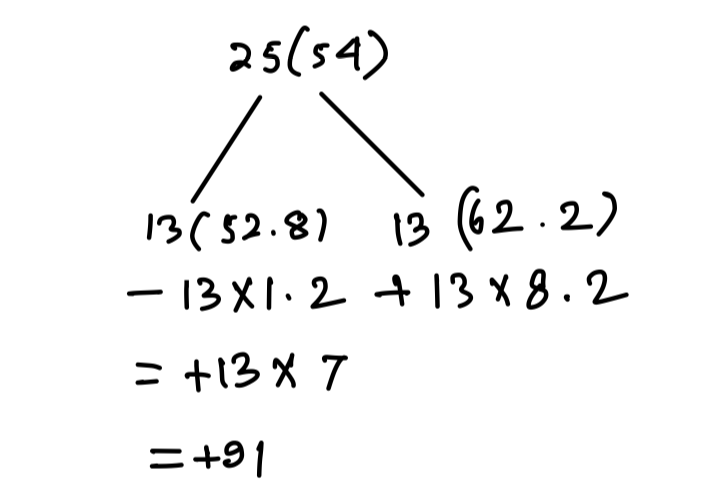
13^th No = 54 + 91 = 145

Now, we have to find out average of 24 No excluding 13^th

\begin{align*} \text{Required Avg} &= \frac{25\times 54-145}{24}\\ &=\frac{1350-145}{24}\\ &=\frac{1205}{24}\\ &=50.2\\ \end{align*}

Q4. The average ages of Kishore, his wife and their child 6 years ago was 38 years and that of his wife and their child 8 years ago was 32 years. Find the present age of Kishore.
(a) 52 years
(b) 48 years
(c) 50 years
(d) 55 years
{Held on: Nov 15, 2020}

Ans: (a) 52 years

Explanation:

At present
K + W + C = 3 × 44 = 132
W + C = 2 × 40 = 80

∴ K = 52

Background concept

Q5. The average of five positive numbers is 56. If the first number is three-fourth of the sum of the last four numbers, then the average of the last four numbers is:
(a) 40
(b) 30
(c) 35
(d) 50
{Held on: Nov 15, 2020}

Ans: (a) 40

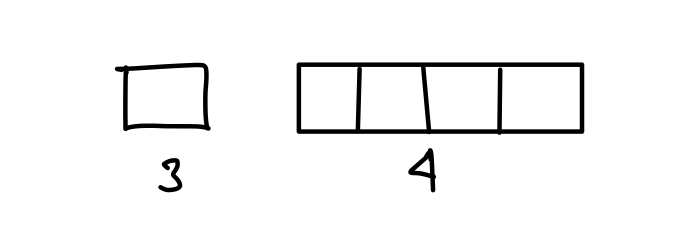
7 part = 5 × 56
1 part = 40

SSC CGL MAINS 2018

Q1. The average of thirteen numbers is 47. The average of the first three numbers is 39 and that of the next seven numbers is 49. The 11^th number is two times the 12^th number and the 12^th number is 3 less than the 13^th number. What is the average of 11^th and 13^th numbers?
(a) 54.5
(b) 55.5
(c) 57
(d) 56
{Held on: Sept. 11, 2019}

Ans: (c) 57

Explanation:

\begin{align*} & 4x-9 = 141+10 \\ &⇒ 4x =160 \\ &⇒ x= 40 \\ \end{align*}

\begin{align*} \text{Required Avg} &= \frac{2x-6+x}{2}\\ &= \frac{3x-6}{2} \\ &= \frac{120-6}{2} \\ &= 57 \\ \end{align*}

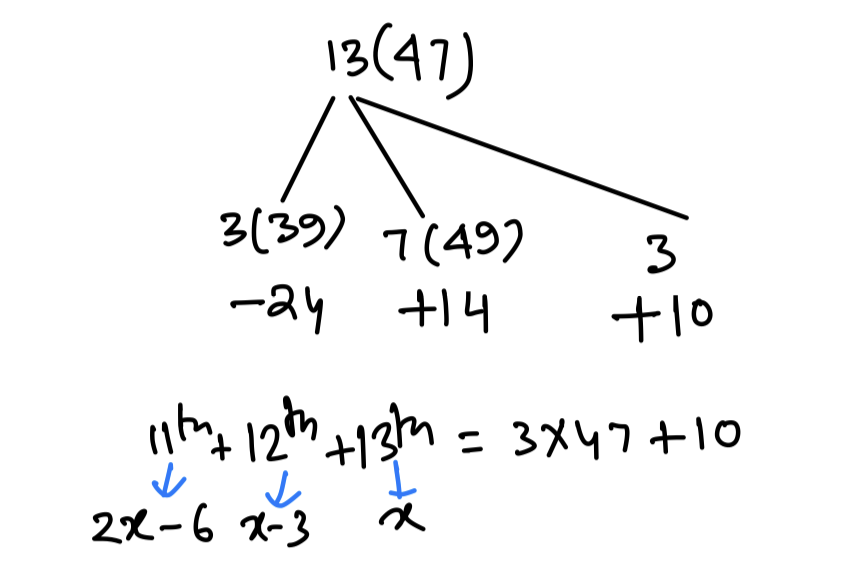
Q2. The average weight of a certain number of students in a group is 72 kg. If 10 students having an average weight of 78kg. leave and 4 students having an average weight of 80 kg join the group, the average weight of the students in the group decreases by 0.7 kg. The number of students initially in the group is:
(a) 56
(b) 46
(c) 44
(d) 54
{Held on: Sept. 12, 2019}

Ans: (b) 46

Explanation:

Initial students = x
Sum = 72x

\begin{align*} & 72x-10\times 78+4\times 80 = (x-10+4)(72-0.7) \\ & ⇒72x- 780+320 = 71.3(x-6) \\ & ⇒72x- 460 = 71.3x-427.8 \\ & ⇒0.7x = 32.2 \\ & ⇒x = 46 \\ \end{align*}

Q3. The average of 33 numbers is 74. The average of the first 17 numbers is 72.8 and that of the last 17 numbers is 77.2 If the 17^th number is excluded, then what will be the average of the remaining numbers (correct to one decimal place)?
(a) 72.9
(b) 73.4
(c) 71.6
(d) 70.8
{Held on: Sept. 12, 2019}

Ans: (a) 72.9

Explanation:

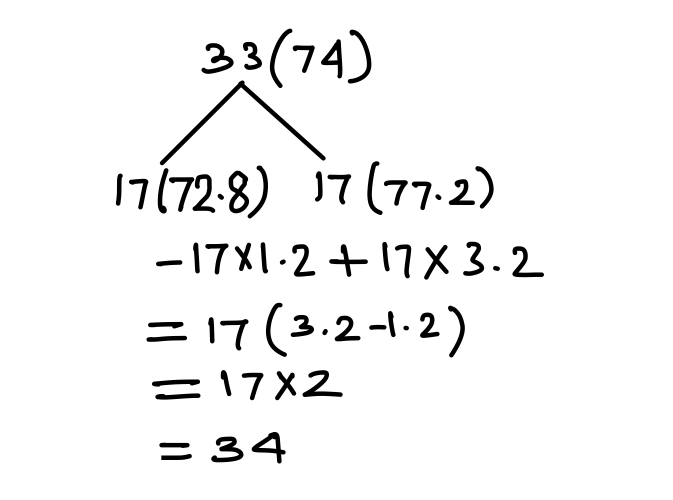
17^th No = 74 + 34 = 108

Now, we have to find out average of 32 No excluding 17^th

\begin{align*} \text{Required Avg} &= \frac{33\times 74-108}{32}\\ &=\frac{1221-54}{16}\\ &=\frac{1167}{16}\\ &=72.2\\ \end{align*}

Q4. The average age of 120 students in a group is 13.56 years. 35% of the number of students are girls and the rest are boys. If the ratio of the average age of boys and girls is 6 : 5, then what is the average age (in years) of the girls?
(a) 12
(b) 11.6
(c) 10
(d) 14.4
{Held on: Sept. 13, 2019}

Ans: (a) 12

Explanation:

\begin{align*} & 7\times 5x +13\times 6x = 20\times 13.56 \\ &⇒ 35x+78x=271.2\\ &⇒ 113x=271.2\\ \end{align*}

\begin{align*} ⇒ 5x & =\frac{271.2\times 5}{113}\\ &=\frac{1356}{113}\\ &=12\\ \end{align*}

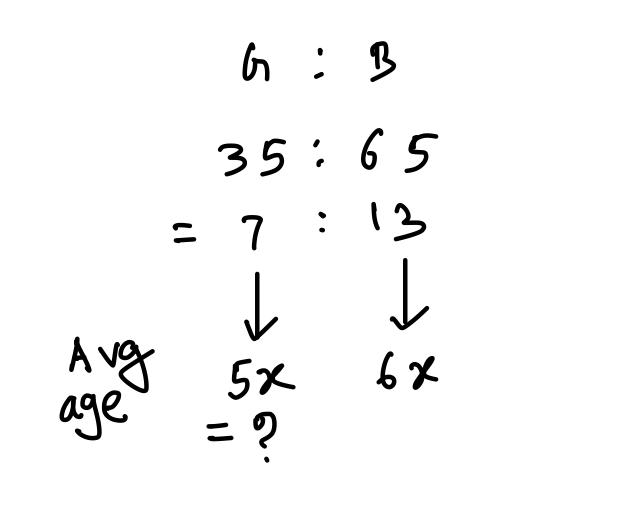
Q5. The average of 18 numbers is 37.5. If six numbers of average x are added to them, then the average of all the numbers increases by one. The value of x is :
(a) 40
(b) 41.5
(c) 42
(d) 38.5
{Held on: Sept. 13, 2019}

Ans: (b) 41.5

Explanation:

\begin{align*} & \frac{6(x-37.5)}{24} = 1 \\ &⇒ x =41.5\\ \end{align*}

Aliter

Sum of new 6 numbers,

\begin{align*} \text{Sum} &= 37.5\times 6+1\times 24\\ &= 225+ 24\\ &= 249\\ \end{align*}

x = \text{Avg} = \frac{249}{6}=41.5

SSC CGL MAINS 2017

Q1. The average marks of 50 students in an examination was 65. It was later found that the marks of one student had been wrongly entered as 83 instead of 38. The correct average is:
(a) 63.9
(b) 64.5
(c) 64.7
(d) 64.1
{Held on: Feb 17, 2018}

Ans: (d) 64.1

Explanation:

Extra taken = 83 – 38 = 45

\begin{align*} \text{Actual avg} &= 65-\frac{45}{50}\\ &= 65-0.9\\ &= 64.1\\ \end{align*}

Q2. The average of 41 consecutive odd numbers is 49. What is the largest number?
(a) 89
(b) 91
(c) 93
(d) 95
{Held on: Feb 17, 2018}

Ans: (a) 89

Explanation:

n = 41
n – 1 = 40
Largest No = 49 + 40 = 89

Q3. A batsman scores 87 runs in the 21st match of his career. His average runs per match increases by 2. What was his average before the 21^st match?
(a) 45
(b) 46
(c) 44
(d) 43
{Held on: Feb 17, 2018}

Ans: (a) 45

Explanation:

87 – 21 × 2 = 87 – 42 = 45

Q4. The average weight of P, Q and R is 71 kg. If the average weight of P and Q be 66 kg and that of Q and R be 76.5 kg, then the weight (in kg) of Q is:
(a) 60
(b) 72
(c) 81
(d) 75
{Held on: Feb 18, 2018}

Ans: (b) 72

Explanation:

P + Q + R = 213 _____(1)
P + Q = 132 _____(2)
Q + R = 153 _____(3)

(2) + (3) – (1) ⟶
Q = 285 – 213
= 72

Q5. Rita buys 5 sarees at an average cost of ₹ 2250. If she buys three more sarees at an average cost of ₹ 2750, what will be the average (in ₹) of all the sarees she buys?
(a) 2437.5
(b) 2500
(c) 2450
(d) 2332.5
{Held on: Feb 18, 2018}

Ans: (a) 2437.5

Explanation:

\begin{align*} \text{Avg price} &=\frac{5\times 2250+3\times 2750}{8}\\ &= \frac{11250+8250}{8}\\ &= \frac{19500}{8}\\ &= 2437.5\\ \end{align*}

Q6. In a one day match of 50 overs, in an innings, the team A had a run rate of 5.3 runs per over. Team B is playing and 5 overs are left and the required run rate to tie the match is 7.2 per over to match the score of Team A. What is team B’s score?
(a) 265
(b) 238
(c) 254
(d) 229
{Held on: Feb 18, 2018}

Ans: (d) 229

Explanation:

Runs by team A = 50 × 5.3 = 265
Team B’s score = x

∴ x + 5 × 7.2 = 265
⇒ x = 265 – 36
= 229

Q7. The average of all even numbers between 104 and 148 is
(a) 128
(b) 130
(c) 124
(d) 126
{Held on: Feb 18, 2018}

Ans: (d) 126

Explanation:

First No = 106
Last No = 146

\begin{align*} \text{Avg} &=\frac{\text{first term}+\text{last term}}{2}\\ &= \frac{106+146}{2}\\ &= \frac{252}{2}\\ &= 126\\ \end{align*}

Q8. The average marks of 18 students in an examination were 60. It was later found that the marks of one student had been wrongly entered as 63 instead of 36. The correct average is:
(a) 59
(b) 59.5
(c) 58
(d) 58.5
{Held on: Feb 19, 2018}

Ans: (d) 58.5

Explanation:

Extra taken = 63 – 36 = 27

\begin{align*} \text{Actual avg} &= 60-\frac{27}{18}\\ &= 60-1.5\\ &= 58.5\\ \end{align*}

Q9. The average of 44 consecutive odd numbers is 144. What is the largest number?
(a) 189
(b) 191
(c) 187
(d) 193
{Held on: Feb 19, 2018}

Ans: (c) 187

Explanation:

Largest No = 144 + 43 = 187

Q10. A batsman makes 100 runs in the 25^th match of his career. His average runs per match increases by 1.4. Find his average before the 25^th match.
(a) 65
(b) 55
(c) 75
(d) 45
{Held on: Feb 19, 2018}

Ans: (a) 65

Explanation:

Required avg
= 100 – 1.4 × 25
= 100 – 35
= 65

Q11. Of the 3 numbers whose average is 22, the first is 3/8th the sum of other two. What is the first number?
(a) 16
(b) 20
(c) 22
(d) 18
{Held on: Feb 20, 2018}

Ans: (d) 18

Explanation:

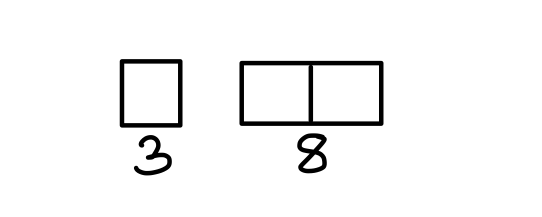
11 part = 3 × 22
3 part = 18

Q12. The average of three consecutive odd numbers is 52 more than 1/3rd of the largest of these numbers. What is the smallest of these numbers?
(a) 79
(b) 75
(c) 81
(d) 77
{Held on: Feb 20, 2018}

Ans: (d) 77

Explanation:

\begin{align*} & x = 52+\frac{1}{3}(x+2)\\ & ⇒ 3x=156+x+2\\ & ⇒ 2x=158\\ & ⇒ x=79\\ \end{align*}

\begin{align*} \therefore x-2=77 \end{align*}

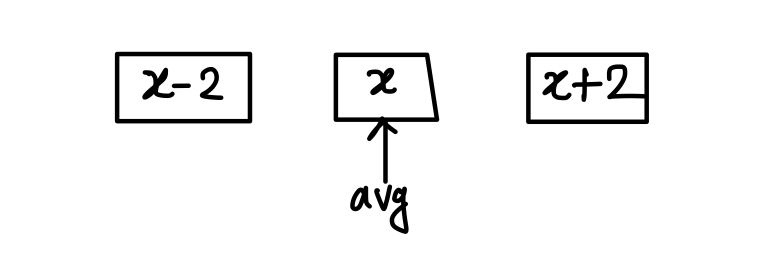
Q13. A batsman scores 98 runs in the 17^th match of his career. His average runs per match increased by 2.5. What is his average before the 17th match?
(a) 58
(b) 60.5
(c) 63
(d) 55.5
{Held on: Feb 20, 2018}

Ans: (d) 55.5

Explanation:

Average was
= 98 – 2.5 × 17
= 98 – 42.5
= 55.5

Q14. What is the average of all numbers between 100 and 200 which are divisible by 13?
(a) 147.5
(b) 145.5
(c) 143.5
(d) 149.5
{Held on: Feb 20, 2018}

Ans: (d) 149.5

Explanation:

100 mod 13 = 9
First No = 100 – 9 + 13 = 104

By mod we have to find remainder. In this case we need to find remainder when 100 is divided by 13

200 mod 13 = 5
Last No = 200 – 5 = 195

\begin{align*} \text{Avg} &=\frac{\text{first term}+\text{last term}}{2}\\ &= \frac{104+195}{2}\\ &= \frac{299}{2}\\ &= 149.5\\ \end{align*}

Q15. The average weight of L, M and N is 93 kg. If the average weight of L and M be 89 kg and that of M and N be 96.5 kg, then the weight (in kg) of M is __________.
(a) 92
(b) 86
(c) 101
(d) 95
{Held on: Feb 21, 2018}

Ans: (a) 92

Explanation:

L + M + N = 279 _____(1)
L + M = 178 _____(2)
M + N = 193 _____(3)

(2) + (3) – (1) ⟶
M = 371 – 279
= 92

Q16. Mahesh buys 3 shirts at an average price of Rs. 1250. If he buys 2 more shirts at an average price of Rs. 1450, what will be the average price (in Rs) of all the 5 shirts he buys?
(a) 1370
(b) 1330
(c) 1310
(d) 1390
{Held on: Feb 21, 2018}

Ans: (b) 1330

Explanation:

\begin{align*} \text{Avg price} &=\frac{3\times 1250+2\times 1450}{3+2}\\ &= \frac{3750+2900}{5}\\ &= \frac{6650}{5}\\ &= 1330\\ \end{align*}

Q17. In a one day match of 50 overs, in an innings, the team A had a run rate of 5.3 runs per over. Team B is playing and 5 overs are left and the required run rate to tie the match is 7.2 per over to match the score of Team A. What is team B’s score?
(a) 235
(b) 230
(c) 240
(d) 225
{Held on: Feb 21, 2018}

Ans: (c) 240

Explanation:

Team A’s score = 50 × 6.1 = 305
Let, team B’s score = x

∴ x + 10 × 6.5 = 305
⇒ x + 65 = 305
⇒ x = 240

Q18. Average of all even numbers between 222 and 250 is __________.
(a) 234
(b) 232
(c) 236
(d) 230
{Held on: Feb 21, 2018}

Ans: (c) 236

Explanation:

First No = 224
Last No = 248

\begin{align*} \text{Avg} &=\frac{\text{first term}+\text{last term}}{2}\\ &= \frac{224+248}{2}\\ &= \frac{472}{2}\\ &= 236\\ \end{align*}

Q19. The average weight of X, Y and Z is 74 kg. If the average weight of X and Y be 68 kg and that of Y and Z be 78 kg, then the weight (in kg) of Y is __________.
(a) 72
(b) 70
(c) 68
(d) 66
{Held on: Mar 9, 2018}

Ans: (b) 70

Explanation:

X + Y + Z = 222 _____(1)
X + Y = 136 _____(2)
Y + Z = 156 _____(3)

(2) + (3) – (1) ⟶
Y = 282 – 222
= 70

Q20. Of the 3 numbers whose average is 26, the first is 2/11 times the sum of the other two. The first number is:
(a) 16
(b) 13
(c) 11
(d) 12
{Held on: Mar 9, 2018}

Ans: (d) 12

Explanation:

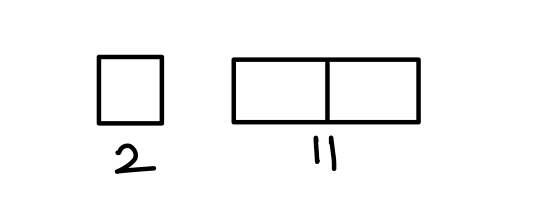
13 part = 3 × 26
2 part = 12

Q21. The average weight of a class of 50 students is 48.6 kg. If the average weight of the 20 boys is 54 kg, then find the average weight (in kg) of the girls in the class.
(a) 40
(b) 46
(c) 45
(d) 42
{Held on: Mar 9, 2018}

Ans: (c) 45

Explanation:

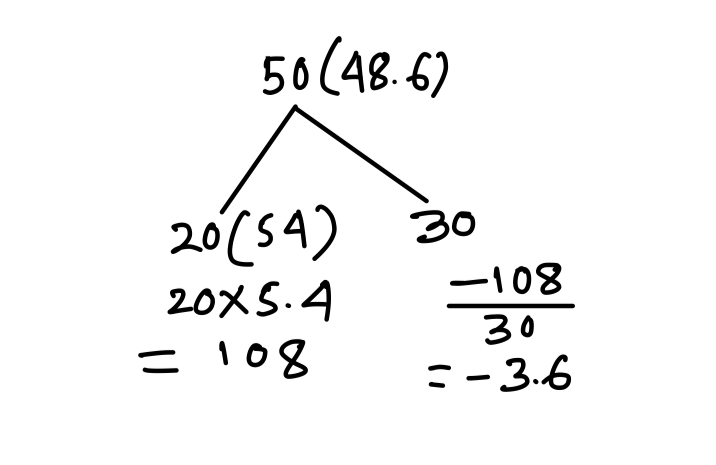
Avg weight of girls
= 48.6 – 3.6
= 45

Q22. The average of all odd numbers from 113 to 159 is __________.
(a) 135
(b) 134
(c) 133
(d) 136
{Held on: Mar 9, 2018}

Ans: (d) 136

Explanation:

First No = 113
Last No = 159

\begin{align*} \text{Avg} &=\frac{\text{first term}+\text{last term}}{2}\\ &= \frac{113+159}{2}\\ &= \frac{272}{2}\\ &= 136\\ \end{align*}

Q23. The average of 35 consecutive even numbers is 44. Find the smallest number.
(a) 8
(b) 12
(c) 10
(d) 14
{Held on: Mar 9, 2018}

Ans: (c) 10

Explanation:

Smallest No = 44 – 34 = 10

Q24. A zoo has an average of 500 visitors on Sundays and 200 on other days. The average number of visitors per day in a month of 30 days beginning with a Sunday is:
(a) 225
(b) 275
(c) 300
(d) 250
{Held on: Mar 9, 2018}

Ans: (d) 250

Explanation:

Dates of month with Sundays = 1, 8, 15, 22, 29

S = 5 days, Avg = 500
O = 25 days, Avg = 200

Now we have to find out monthly average visitors per day.

\begin{align*} \text{Avg} &=\frac{5\times 500+25\times 200}{30}\\ &= \frac{2500+5000}{30}\\ &= \frac{7500}{30}\\ &= 250\\ \end{align*}

Q25. In a club there are 12 wrestlers. When a wrestler whose weight is 90 kg leaves the club, he is replaced by a new wrestler then the average weight of this 12 member club increases by 0.75 kg. What is the weight (in kg) of the new wrestler who joined the club?
(a) 108
(b) 99
(c) 112
(d) 100
{Held on: Mar 9, 2018}

Ans: (b) 99

Explanation:

Weight of new wrestler
= 90 + 0.75 × 12
= 90 + 9
= 99

Q26. In a set of three numbers, the average of first two numbers is 21, the average of the last two numbers is 24, and the average of the first and the last numbers is 15. What is the average of three numbers?
(a) 20
(b) 60
(c) 25
(d) 18
{Held on: Mar 9, 2018}

Ans: (a) 20

Explanation:

Let, the numbers are x, y and z

x + y = 42 _____(1)
y + z = 48 _____(2)
x + z = 30 _____(3)

By adding all three equations,
2(x +y + z) = 120

⇒ x +y + z = 60

⇒ $\displaystyle\frac{\text{x +y + z}}{3}$ = 20

SSC CGL MAINS 2016

Q1. A and B have their annual average income ₹80,000. B and C have their annual average income ₹75,000. C and A have their annual average income ₹78,000. The annual income of A is?
(a) ₹81000
(b) ₹82000
(c) ₹83000
(d) ₹84000
{Held on: Nov 30, 2016}

Ans: (c) ₹83000

Explanation:

A + B = 160k _____(1)
B + C = 150k _____(2)
C + A = 156k _____(3)

By adding all three equations,
2(A + B + C) = 466k
⇒ A + B + C = 233k
⇒ A + 150k = 233k [Since B + C = 150k]
⇒ A = 83k = 83000

Q2. In the first 10 overs of a cricket game, the run rate was only 3.2. What should be the run rate in the remaining 40 overs to reach the target of 282 runs?
(a) 6.4
(b) 6.3
(c) 6.25
(d) 6.5
{Held on: Nov 30, 2016}

Ans: (c) 6.25

Explanation:

10 × 3.2 + 40x = 282
⇒ 32 + 40x = 282
⇒ 40x = 250
⇒ x = 6.25

Q3. The average (arithmetic mean) amount of savings of ten students is Rs. 600. Three of the students have no savings at all and each of the others have at least Rs. 250 including Nihar, who has exactly Rs. 1300. The largest amount, in Rs., that anyone student could have is
(a) 3250
(b) 3450
(c) 3650
(d) 3850
{Held on: Nov 30, 2016}

Ans: (b) 3450

Explanation:

Average of 10 students = 600
∴ Sum = 6000

Among them three has no savings at all.
Hence, 7 has this ₹6000

Sum (7 students) = 6000
Nihar has exactly 1300
∴ Sum (6 students) = 6000 – 1300 = 4700

They have ≥ 250
To be max, we will assign 5 students at min i.e. 250

Hence, max = 4700 – 250 × 5 = 4700 – 1250 = 3450

Q4. An Army of 12000 consists of Europeans and Indians. The average height of a European is 5ft 10 inches and that of an Indian is 5ft 9 Inches and that of the whole army is 5ft $9\displaystyle\frac{3}{4}$ inches. Then the number of Indians in the army is?
(a) 3000
(b) 4000
(c) 5500
(d) 2700
{Held on: Nov 30, 2016}

Ans: (a) 3000

Explanation:

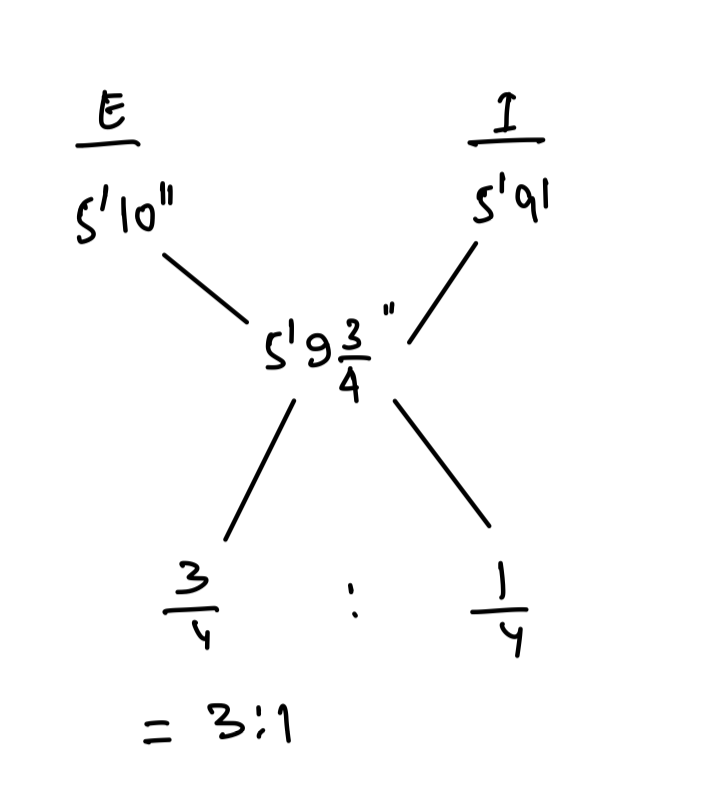
4 part = 12000
1 part = 3000

Q5. The sum of three consecutive even numbers is 28 more than the average of these three numbers. The smallest of these three number is:
(a) 6
(b) 12
(c) 14
(d) 16
{Held on: Dec 1, 2016}

Ans: (b) 12

Explanation:

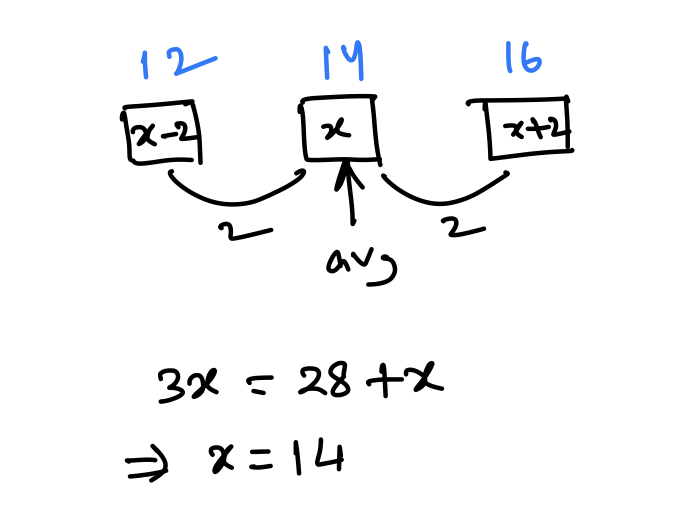
Q6. Fifteen movie theatres average 600 customers per theatre per day. If six of the theatres close down but the total theatre attendance stays the same, then the average daily attendance per theatre among the remaining theatres is
(a) 900
(b) 1000
(c) 1100
(d) 1200
{Held on: Dec 1, 2016}

Ans: (b) 1000

Explanation:

n = 15, Avg = 600
Total Customer per day = 15 × 600 = 9000

6 theatres close down
Now no of theatres = 15 – 6 = 9
But customer remain same

So, daily average attendance = $\displaystyle\frac{9000}{9}$ = 1000

Q7. The average weight of A, B and C is 45 kg. If the average weight of A and B be 40 kg and that of B and C be 43 kg, then the weight of B is :
(a) 31 kg
(b) 32 kg
(c) 29.5 kg
(d) 35 kg
{Held on: Dec 1, 2016}

Ans: (a) 31 kg

Explanation:

A + B + C = 135 _____(1)
A + B = 80 _____(2)
B + C = 86 _____(3)

(2) + (3) – (1) ⟶
B = 166 – 135
= 31

Q8. The batting average for 40 innings of a cricket player is 50 runs. His highest score exceeds his lowest score by 172 runs. If these two innings are excluded, the average of the remaining 38 innings is 48 runs. The highest score of the player is
(a) 165
(b) 170
(c) 172
(d) 174
{Held on: Dec 1, 2016}

Ans: (d) 174

Explanation:

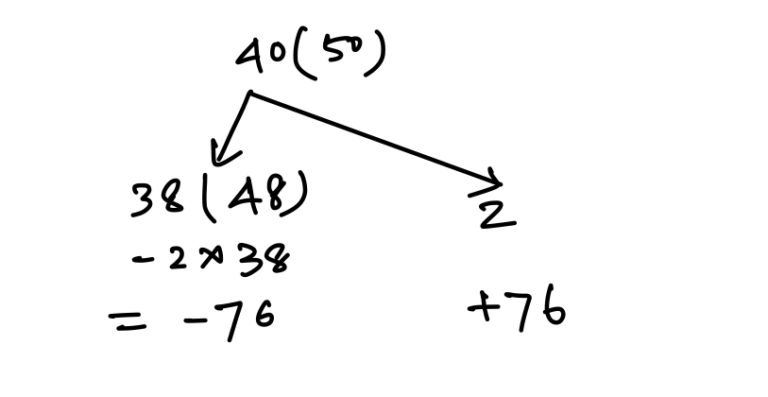
Sum (2 match) = 2 × 50 + 76 = 176
Now, 176 = 2 + 174

So, highest score = 174

Q9. The average of 7 consecutive numbers is 20. The largest of these numbers is
(a) 20
(b) 23
(c) 24
(d) 26
{Held on: Dec 1, 2016}

Ans: (b) 23

Explanation:

4^th no = avg = 20

Largest no (7^th) = 20 + 3 = 23

Q10. Mukesh has twice as much money as Soham. Soham has 50% more money than Pankaj. If the average money with them is Rs. 110, then Mukesh has
(a) 155
(b) 160
(c) 180
(d) 175
{Held on: Dec 1, 2016}

Ans: (c) 180

Explanation:

50% = $\displaystyle\frac{1}{2}$ ⇒ 1 more on 2

11 part = 3 × 110
6 part = 180

Q11. The average daily income of 7 men, 11 women and 2 boys is Rs. 257.50. If the average daily income of the men is Rs. 10 more than that of women and the average daily income of the women is Rs. 10 more than that of boys, the average daily income of a man is
(a) ₹277.5
(b) ₹250
(c) ₹265
(d) ₹257
{Held on: Dec 1, 2016}

Ans: (c) ₹265

Explanation:

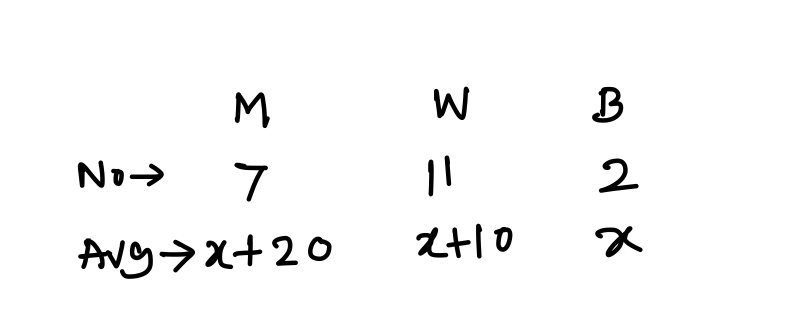
7(x + 20) + 11(x + 10) + 2x = 20 × 257.50
⇒ 7x + 140 + 11x + 110 + 2x = 20 × 257.5
⇒ 20x + 250 = 20 × 257.5
⇒ 2x + 25 = 515 [By dividing both side by 10]
⇒ 2x = 490
⇒ x = 245

∴ x + 20 = 265

Q12. A batsman has a certain average of runs for 12 innings. In the 13th innings, he scores 96 runs and thereby increasing his average by 5 runs. What is his average after the 13th innings?
(a) 28
(b) 32
(c) 36
(d) 42
{Held on: Jan 12, 2017}

Ans: (c) 36

Explanation:

Avg till 12th innings = 96 – 5 × 13 = 96 – 65 = 31

Average after 13th innings = 31 +5 = 36

Q13. A team of 8 persons joins a shooting competition. The best marksman scored 85 points. If he had scored 92 points, then the average score for the team would have been 84. The number of points the team scored was
(a) 672
(b) 665
(c) 645
(d) 588
{Held on: Jan 12, 2017}

Ans: (b) 665

Explanation:

92 – 85 = 7

When avg becomes 84, only 7 is added in the previous sum

So, previous sum = 8 × 84 – 7 = 672 – 7 = 665

Aliter (By Traditional Method)

Let the previous avg = x
Sum = 8x
Here score of top marksman = 85
So, score by rest = 8x – 85

For second case,
Sum = 8 × 84 = 672
Score of top marksman = 92
Score by rest = 672 – 92 = 580

∴ 8x – 85 = 580
⇒ 8x = 665

Q14. A librarian purchased 60 story books for his library. But he found that he could get 4 extra books by spending Rs 336 more and then the overall average price per book would be reduced by Re 1. The previous average price of each book was
(a) ₹84
(b) ₹83
(c) ₹68
(d) ₹100
{Held on: Jan 12, 2017}

Ans: (d) ₹100

Explanation:

60 books, avg = x ⇒ sum = 60x
64 books, avg = x – 1 ⇒ sum = 64x -64
And price of extra 4 books is 336

∴ 64x – 64 – 60x = 336
⇒ 4x = 400
⇒ x = 100

Q15. In an exam, the average marks obtained by John in English, Maths, Hindi and Drawing were 50. His average marks in Maths, Science, Social Studies and Craft were 70. If the average marks in all seven subjects is 58, his score in maths was
(a) 50
(b) 52
(c) 60
(d) 74
{Held on: Jan 12, 2017}

Ans: (d) 74

Explanation:

E + M + H + D = 200 _____(1)
M + S + SS + C = 280 _____(2)
E + M + H + D +S + SS + C = 58 × 7 = 406 _____(3)

(1) + (2) – (3) ⟶
M = 480 – 406
= 74

Q16. The average weight of 3 men A , B, and C is 84 kg. D joins them and the average weight of the four becomes 80 kg. If E whose weight is 3 kg more than that of D replaces A, the averages weight of B, C , D and E becomes 79 kg. The weight of A is
(a) 70 kg
(b) 72 kg
(c) 75 kg
(d) 80 kg
{Held on: Jan 12, 2017}

Ans: (c) 75 kg

Explanation:

A + B + C = 3 × 84 = 252 _____(1)
A + B + C + D = 4 × 80 = 320 _____(2)

(2) – (1) ⟶
D = 68
∴ E = 68 + 3 = 71

B + C + D + E = 4 × 79 = 316
⇒ B + C + 68 + 71 = 316
⇒ B + C + 139 = 316
⇒ B + C = 177

Putting B + C = 177 in eqⁿ (1)
A = 252 – 177 = 75

SSC CGL MAINS 2015

Q1. The average of five consecutive positive integers is n. If the next two integers are also included, the average of all these integers will
(a) Increase by 1.5
(b) Increase by 2
(c) Increase by 1
(d) Remain the same
{Held on: Aug 25, 2015}

Ans: (c) Increase by 1

Explanation:

The numbers will form a AP Series.

Avg(5 Numbers) = 3^rd No
Avg(7 Numbers) = 4^th No

Here difference is 1.
So, avg will increase by 1.

Q2. Average of $n$ numbers is $a$ . The first number is increased by 2, second one is increased by 4, the third one is increased by 8 and so on. The average of the new numbers is

(a) $a+\displaystyle\frac{2^{n-1}}{n}$

(b) $a+\displaystyle\frac{2^n-1}{n}$

(c) $a+\displaystyle\frac{2^{n+1}-1}{n}$

(d) $a+2\displaystyle\frac{2^n-1}{n}$

{Held on: Aug 25, 2015}

Ans: (d) $a+2\displaystyle\frac{2^n-1}{n}$

Explanation:

Increment in Sum
= 2 + 4 + 8 + ∙∙∙ + n^th increment

= 2¹ + 2² + 2³ + ∙∙∙ + 2ⁿ

= $\displaystyle\frac{2(2^n-1)}{2-1}$

= 2(2ⁿ – 1)

Note: 2¹ + 2² + 2³ + ∙∙∙ + 2ⁿ is a GP series with r = 2 and a = 2

Sum of GP series = $\displaystyle\frac{a(r^n-1)}{r-1}$

Increment in avg = $\displaystyle\frac{2(2^n-1)}{n}$

∴ New avg = Old avg + increased avg = $a+2\displaystyle\frac{2^n-1}{n}$

Q3. Three science classes A, B and C take a life science test. The average score of class A is 83. The average score of class B is 76. The average score of class C is 85. The average score of class A and B is 79 and average score of class B and C is 81. Then the average score of classes A, B and C is
(a) 81.5
(b) 80
(c) 81
(d) 80.5
{Held on: Aug 25, 2015}

Ans: (a) 81.5

Explanation:

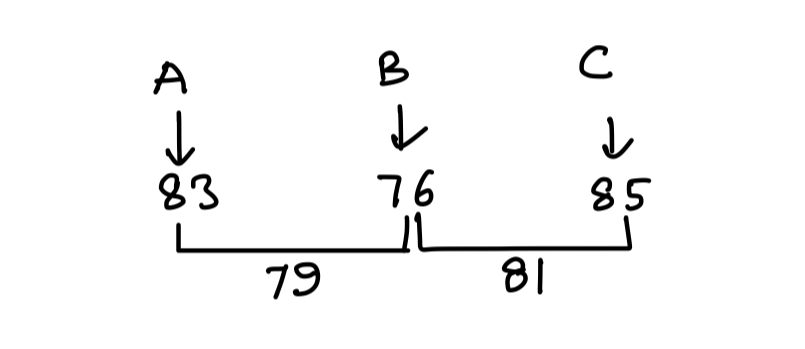
By Alligation:

n_A : n_B = 3 : 4
n_B : n_C = 4 : 5

∴ n_A : n_B : n_C= 3 : 4 : 5

\begin{align*} \text{Avg Score} &= \frac{3\times 83+4 \times 76 + 5\times 85}{3+4+5}\\ &= \frac{249+304+425}{12} \\ &= \frac{978}{12} \\ &= 81.5 \\ \end{align*}

Q4. The average age of 30 students of a class is 14 years 4 months. After admission of 5 new students in the class the average becomes 13 years 9 months. The youngest one of the five new students is 9 years 11 months old. The average age of the remaining 4 new students is
(a) 12 years 4 months
(b) 11 years 2 months
(c) 10 years 4 months
(d) 13 years 6 months
{Held on: Aug 25, 2015}

Ans: (c) 10 years 4 months

Explanation:

We know 1 year = 12 month

For 30 students avg = 14y 4m
For 35 students avg = 13y 9m
Avg is decreased 7m when 5 new members are added.

Sum(5 new students)
= 5 × 14y 4m – 35 × 7m
= 860m – 245m
= 615m

Youngest member = 9y 11m = 119m

∴ Sum(Rest 4 students)
= 615m – 119m
= 196m

Hence avg of them = $\displaystyle\frac{496\text{m}}{4}$ = 124m = 10y 4m

SSC CGL MAINS 2014

Q1. The average weight of first 11 persons among 12 persons is 95 kg. The weight of 12^th person is 33 kg more than the average weight of all the 12 persons. The weight of the 12^th person is
(a) 128 kg
(b) 97.45 kg
(c) 128.75 kg
(d) 131 kg
{Held on: Apr 12, 2015}

Ans: (d) 131 kg

Explanation:

n = 12, avg = x ⇒ sum = 12x
n = 11, avg = 95 ⇒ sum = 11 × 95

x + 33 = ?

12x – 11 × 95 = x + 33
⇒ 11x = 11 × 95 + 11 × 3
⇒ x = 98 [by dividing both side by 11]

∴ x + 33 = 98 +33 = 131

Q2. The average of six numbers is 3.95. The average of two of them is 3.4, while the average of the other two is 3.85. The average of the remaining two numbers is
(a) 4.5
(b) 4.7
(c) 4.6
(d) 4.8
{Held on: Apr 12, 2015}

Ans: (c) 4.6

Explanation:

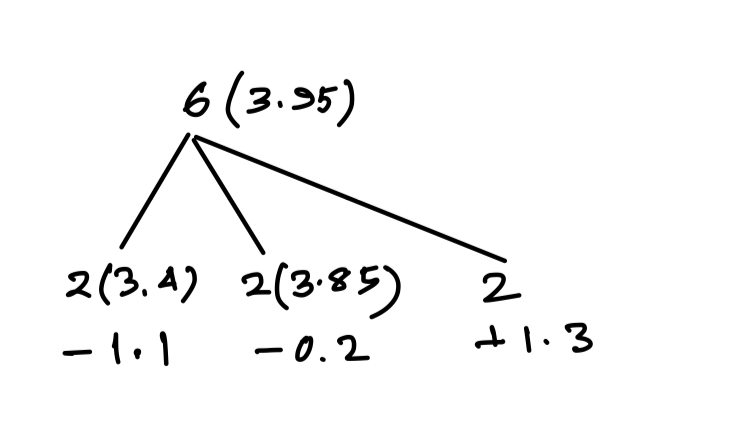
Sum = 2 × 3.95 + 1.3

∴ Avg = 3.95 + 0.65 = 4.6

Q3. If the average of eight consecutive even numbers is 93, then the greatest numbers among them is
(a) 86
(b) 98
(c) 100
(d) 102
{Held on: Apr 12, 2015}

Ans: (c) 100

Explanation:

n – 1 = 8 – 1 = 7

Greatest No = avg + (n – 1) = 93 + 7 = 100

Q4. If the arithmetic mean of 3a and 4b is greater than 50, and a is twice b, then the smallest possible integer value of a is
(a) 18
(b) 19
(c) 20
(d) 21
{Held on: Apr 12, 2015}

Ans: (d) 21

Explanation:

Given data, Avg > 50 and a = 2b

\begin{align*} &\frac{3a+4b}{2}>50 \\ & \Rightarrow 3a+4b>100 \\ & \Rightarrow 3a+4\cdot \frac{a}{2}>100 \\ & \Rightarrow 5a>100 \\ & \Rightarrow a>20 \\ \end{align*}

Hence, a_min = 21

Q5. The average (arithmetic mean) of $3^{30}$ , $3^{60}$ and $3^{90}$ is
(a) $3^{60}$
(b) $3^{117}$
(c) $3^{27}+3^{57}+3^{87}$
(d) $3^{29}+3^{59}+3^{89}$
{Held on: Apr 12, 2015}

Ans: (d) $3^{29}+3^{59}+3^{89}$

Explanation:

Avg = $\displaystyle\frac{3^{30}+3^{60}+3^{90}}{3}$ = $3^{29}+3^{59}+3^{89}$

Q6. Average of 11 numbers is 36, whereas average of 9 of them is 34. If the remaining two numbers are in the ratio 2 : 3, then find the value of the smaller number (between remaining two numbers).
(a) 54
(b) 36
(c) 45
(d) 48
{Held on: Apr 12, 2015}

Ans: (b) 36

Explanation:

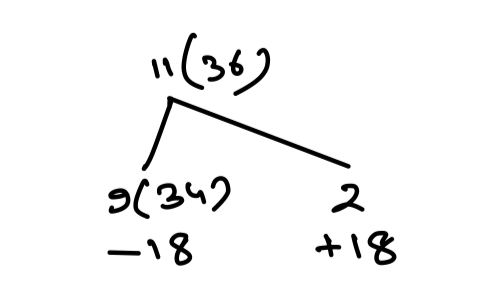
Sum = 2 × 36 + 18 = 72 +18 = 90

Ratio of numbers = 2 : 3

∴ 5 part = 90
⇒ 2 part = 36

Q7. the average of 20 numbers is calculated as 35. it is discovered later on that while calculating the average one number namely 85 was read as 45. the correct average is
(a) 37.5
(b) 36
(c) 36.5
(d) 37
{Held on: Apr 12, 2015}

Ans: (d) 37

Explanation:

85 was read as 45
So, 40 was less taken in sum

Actual avg = 35 + $\displaystyle\frac{40}{20}$ = 37

Q8. Of three numbers, the first is 4 times the second and 3 times the third. If the average of all the three numbers is 95, what is the third number ?
(a) 130
(b) 57
(c) 76
(d) 60
{Held on: Apr 12, 2015}

Ans: (d) 60

Explanation:

I = 4 II = 3 III

∴ I : II : III = 12 : 3 : 4

Now, 19 part = 3 × 95
⇒ 4 part = 60

Q9. If average of two numbers $x$ and $\displaystyle\frac{1}{x}$ (where $x$ ≠ 0) is A, what will be the average of $x^3$ and $\displaystyle\frac{1}{x^3}$ ?
(a) 4A³ – 4A
(b) 4A³ – A
(c) 4A³ – 2A
(d) 4A³ – 3A
{Held on: Apr 12, 2015}

Ans: (d) 4A³ – 3A

Explanation:

x+\frac{1}{x}=2A

\begin{align*} x^3 + \frac{1}{x^3} & = \left(x+\frac{1}{x}\right)^3-3\cdot x\cdot \frac{1}{x}\left(x+\frac{1}{x}\right)\\ &=(2A)^3-3\cdot 2A\\ &=8A^3-6A\\ \end{align*}

Hence avg of $x^3$ and $\displaystyle\frac{1}{x^3}$ = $\displaystyle\frac{8A^3-6A}{2}$ = $4A^3 - 3A$

Q10. The average weight of A, B and C is 45 kg. If the average weight of A and B be 40 kg and that of B and C be 43 kg, then the weight of B is
(a) 31
(b) 17
(c) 20
(d) 26
{Held on: Apr 12, 2015}

Ans: (a) 31

Explanation:

A + B + C = 135 _____(1)
A + B = 80 _____(2)
B + C = 86 _____(3)

(2) + (3) – (1) ⟶
B = 166 – 135
= 31

Q11. In a team of 10 persons, nine persons spent ₹40 each for their meal and the remaining one spent ₹9 more than the average expenditure of all the 10 persons. The total expenditure for their meal was
(a) 410
(b) 610
(c) 510
(d) 310
{Held on: Apr 12, 2015}

Ans: a) 410

Explanation:

Let, avg expenditure of 10 person = x ⇒ Sum = 10x
n = 9, avg = 40 ⇒ sum = 360
Expenditure of 10^th person = x + 9

∴ 10x – 360 = x + 9
⇒ 11x = 369
⇒ x = 49

Total expenditure = 10x = 410

SSC CGL MAINS 2013

Q1. The average of the first three numbers is double of the fourth number. If the average of all the four numbers is 12. Find the 4^th number
(a) 16
(b) 48/7
(c) 20
(d) 18/7
{Held on: Sept. 29, 2013}

Ans: (b) 48/7

Explanation:

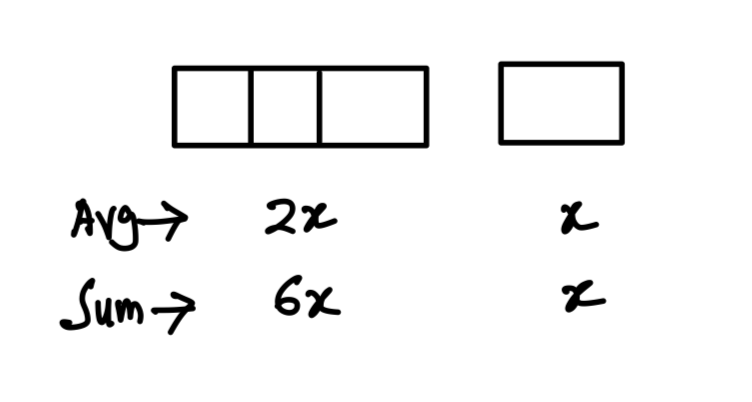
∴ 7x = 4 × 12
⇒ x = 48/7

Q2. If the average of 6 consecutive even numbers is 25, the difference between the largest and the smallest number is
(a) 8
(b) 10
(c) 12
(d) 14
{Held on: Sept. 29, 2013}

Ans: (b) 10

Explanation:

Largest = 6^th No
Smallest = 1^st No

Difference = (6 – 1) × 2 = 10

Q3. The arithmetic mean of 100 observations is 24. 6 is added to each of the observations and then each of them is multiplied by 2.5. Find the new arithmetic mean.
(a) 30
(b) 75
(c) 35
(d) 60
{Held on: Sept. 29, 2013}

Ans: (b) 75

Explanation:

Old avg = 24

New avg = (24 + 6) × 2.5 = 30 × 2.5 = 75

Q4. Sachin Tendulkar has a certain average for 11 innings. In the 12th innings he scores 120 runs and there by increases his average by 5 runs, his new average is
(a) 60
(b) 62
(c) 65
(d) 66
{Held on: Sept. 29, 2013}

Ans: (c) 65

Explanation:

Avg till 11th innings
= 120 – 5 × 12
= 60

Avg after 12th innings
= 60 + 5
= 65

Q5. The average of 11 results is 50. If the average of the first six results is 49 and that of the last six is 52, then the sixth result is
(a) 48
(b) 50
(c) 52
(d) 56
{Held on: Sept. 29, 2013}

Ans: (d) 56

Explanation:

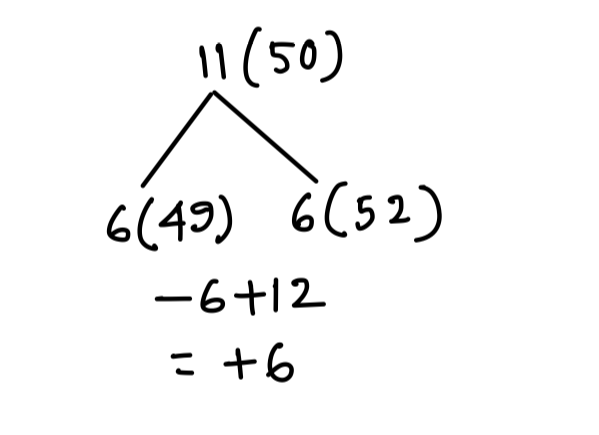
6^th No = 50 + 6 = 56

👉 More on Mathematics for Competitive Exam

Join Us

Join the discussion and ask any question of maths and reasoning directly to us and other like-minded user just like you!

<<Prev

Home

Next>>

Please share this post with someone who might find it helpful.

Previous Year Average Questions For SSC CGL Mains/Tier II till date

SSC CGL MAINS 2020

SSC CGL MAINS 2019

SSC CGL MAINS 2018

SSC CGL MAINS 2017

SSC CGL MAINS 2016

SSC CGL MAINS 2015

SSC CGL MAINS 2014

SSC CGL MAINS 2013

Join Us

Leave a Comment Cancel Reply

About Our Content

SSC CGL MAINS 2020

SSC CGL MAINS 2019

SSC CGL MAINS 2018

SSC CGL MAINS 2017

SSC CGL MAINS 2016

SSC CGL MAINS 2015

SSC CGL MAINS 2014

SSC CGL MAINS 2013

Join Us

RELATED POSTS

Leave a Comment Cancel Reply