Profit and Loss – Dishonest Dealers and Faulty Weights

<<Prev

Home

Next>>

Concepts of Dishonest Dealer

A dishonest dealer is person who gives less weight than actual. So, he gains in weight (weight gain).

If a dishonest dealer sells his product at CP, weight gain will the the only profit. But if he sells the product at a certain profit percentage on CP (monetary gain), his overall profit will be net effect of weight gain and monetary gain.

Methods of Solving Problems on Dishonest Dealer

To solve such problems there are multiple ways. Use whatever is convenient to you.

I personally prefer Method 2: #Quantity – Price

Question: A dishonest shopkeeper sells sugar at Rs. 18/kg which he has bought at Rs. 15/kg and he is giving 800 gm instead of 1000 gm. Find his actual profit percentage.

Ans: 50%

Explanation:

Method 1: Using ab Method

CP = 15, SP = 18

Monetary gain = \displaystyle\frac{3}{15}\times 100 = 20\%

\boxed{\text{Weight Gain} = \frac{\text{Error}}{\text{Faulty weight}}\times 100}

He is giving 800 gm instead 1000 gm

Error = (1000 – 200) gm = 200 gm

Faulty weight = 800g

Weight gain = \displaystyle\frac{200}{800}\times 100 = 25\%

Now applying ab method

(Monetary gain, weight gain) → profit

(20, 25) → 20 + 25 + \displaystyle\frac{20\times 25}{100} = 50%

Method 2: #Quantity – Price

You may consider reading the concept before jumping to solution if you have not gone though this already.

\displaystyle\frac{\text{CP}}{\text{SP}} = \displaystyle\frac{800\times 15}{1000\times 18}  = \displaystyle\frac{2}{3}

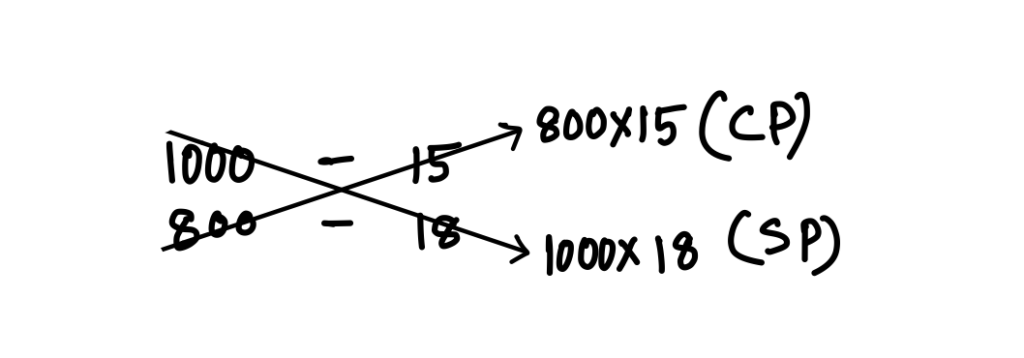
P% = \displaystyle\frac{1}{2}\times 100 = 50\%

Method 3: Using Formula

Overall profit calculation without calculating weight gain

\boxed{\frac{100+\text{G}}{100+\text{x}} =  \frac{\text{True weight}}{\text{False weight}}}

Here, G = overall gain and x = monetary gain/loss%

We have already solved for x = 20%

So,  \displaystyle\frac{100+\text{G}}{100+20} = \displaystyle\frac{1000}{800}

⇒  \displaystyle\frac{100+\text{G}}{120} = \displaystyle\frac{5}{4}

⇒ 100 + G = 150

⇒ G = 50

Actual profit percentage = 50%

Method 4: General approach

For 1kg, CP = 15 and SP = 18

Now, for 800 gm, CP = \displaystyle\frac{15}{1000}\times 800 = 12 (Here we have calculated the CP of 800 gm sugar because the shopkeeper is actually selling only 800gm.)

He is selling 800 gm sugar for Rs 18 for which he had paid Rs 12.

So, P% = \displaystyle\frac{6}{12}\times 100 = 50\%

Question: A shopkeeper claims that he is selling sugar at Rs 23/kg which cost him Rs 25/kg but he is giving 800gm instead of 1000gm. What is his percentage profit or loss?

Ans: 15% profit

Explanation:

SP = 23, CP = 25

L% = \displaystyle\frac{2}{25}\times 100 = 8\%

Weight gain = \displaystyle\frac{200}{800}\times 100 = 25\%

Applying ab method,

(-8, 25) → -8 + 25 + \displaystyle\frac{-8\times 25}{100} = 15%

Hence his percentage profit is 15%.

Question: A dishonest dealer professes to sell his goods at a loss of 10% but uses a weight of 800gm instead of 1 kg. Find his profit or loss%.

Ans: 12.5% profit

Explanation:

Monetary loss = 10%

Weight gain = \displaystyle\frac{200}{800}\times 100 = 25\%

Applying ab method,

(-10, 25) → -10 + 25 + \displaystyle\frac{-10\times 25}{100} = 12.5%

Practicing problems

Question: A shopkeeper uses 940 gm in place of one kg. He sells it at 4% profit. What will be the overall profit?
(a) 10.4%
(b) 10.6%
(c) 10.8%
(d) 10.9%

Ans: (b) 10.6%

Explanation:

\displaystyle\frac{\text{CP}}{\text{SP}} = \displaystyle\frac{940\times 100}{1000\times 104}  = \displaystyle\frac{47}{52}

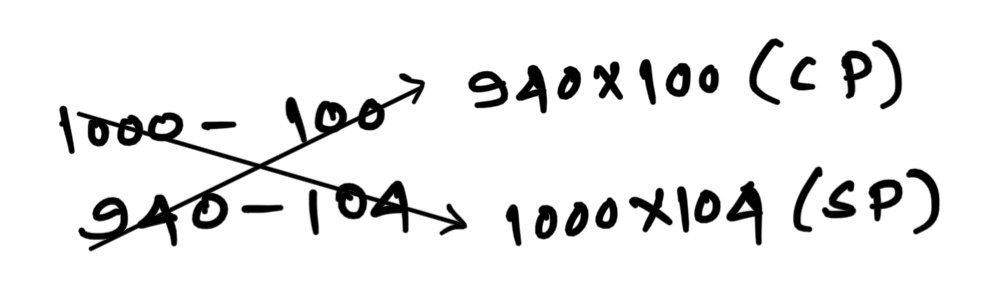
P% = \displaystyle\frac{5}{47}\times 100 = 10.63\% = 10.6\% (rounding off to 1 decimal)

Question: A dishonest dealer sells products at 10% loss on cost price but uses 2 gm instead of 4 gm. what is his profit or loss percent?
(a) 80% profit
(b) 80% loss
(c) 90% profit
(c) 10% loss

Ans: (a) 80% profit

Explanation:

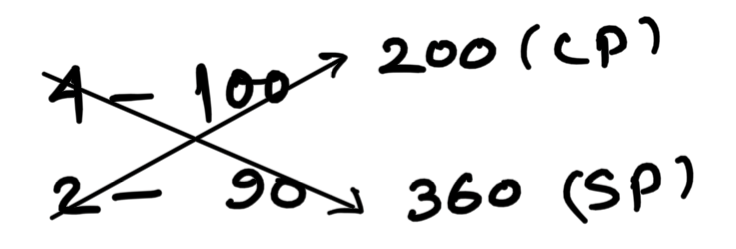
P% = \displaystyle\frac{160}{200}\times 100 = 80\%

Question: A dishonest merchant sells his grocery using weights 15% less than the true weights and makes a profit of 20%. Find his total gain percentage.
(a) 40%
(b) 40.17%
(c) 41%
(d) 41.17%

Ans: (d) 41.17%

Explanation:

Let us assume his CP/100g = ₹100

So, his SP/85g = ₹120

\displaystyle\frac{\text{CP}}{\text{SP}} = \displaystyle\frac{85\times 100}{1000\times 120}  = \displaystyle\frac{17}{24}

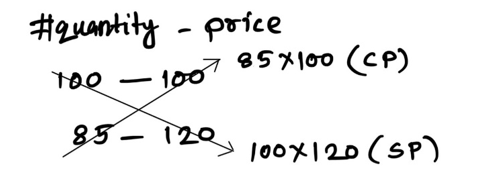
P% = \displaystyle\frac{7}{17}\times 100 = 41.17\%

Question: A shopkeeper sells an item at a profit of 20 % and uses a weight which is 20% less. Find his total profit.
(a) 40%
(b) 45%
(c) 50%
(d) 60%

Ans: (c) 50%

Explanation:

Let us assume his CP/100g = ₹100

So, his SP/850g = ₹120

\displaystyle\frac{\text{CP}}{\text{SP}} = \displaystyle\frac{80\times 100}{100\times 120}  = \displaystyle\frac{2}{3}

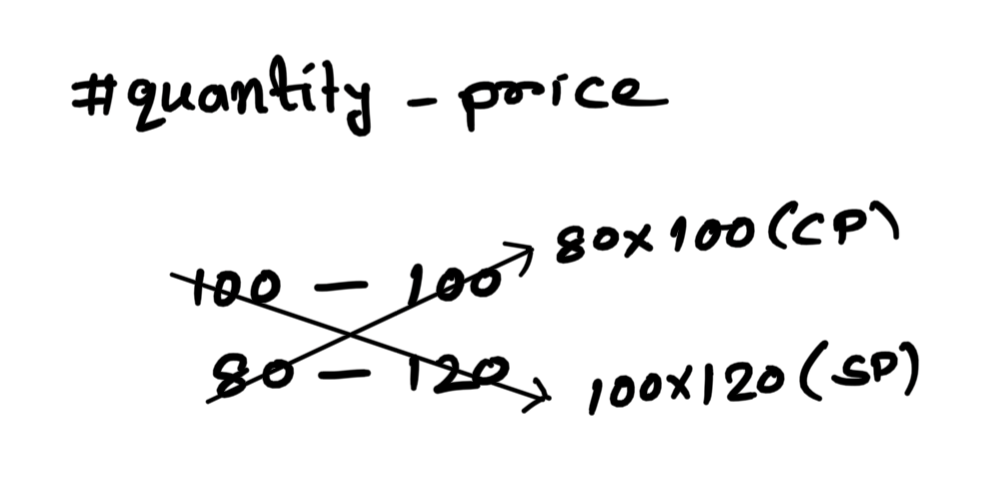
P% = \displaystyle\frac{1}{2}\times 100 = 50\%

Question: A dishonest dealer sells goods at 10% loss on cost price but uses 20% less weight. Calculate profit percent.
(a) 10%
(b) 8%
(c) 12.5%
(d) none of above

Ans: (c) 12.5%

Explanation:

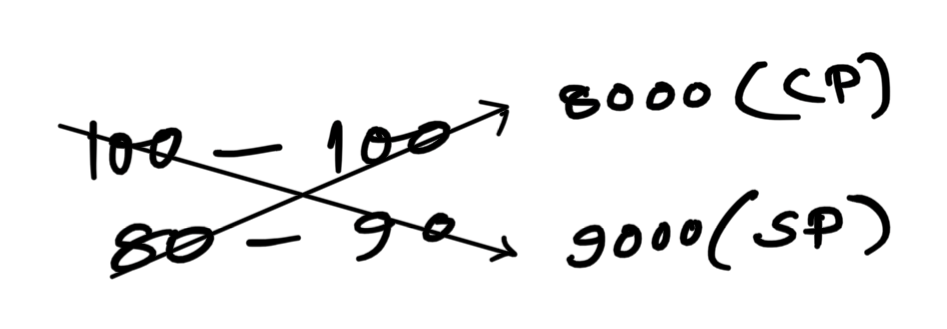
P% = \displaystyle\frac{1000}{8000}\times 100 = 12.5\%

Question: A dishonest dealer professes to sell his good at cost price but uses a false weight and thus gains 20%. For a kilogram he uses a weight of
(a) 700g
(b) 750g
(c) 800g
(d) None of these

Ans: (d) None of these

Explanation:

Weight gain = \displaystyle\frac{\text{Error}}{\text{Faulty wiight}}\times 100

Let, faulty weight is x g

So, \displaystyle\frac{1000-x}{x}\times 100 = 20

⇒ 5000 – 5x = x

⇒ 4x = 5000

⇒ x = 833.33

Question: A dishonest shop keeper professes to sell his goods at the cost price but uses faulty measure. His 1 kg weight measures 950g only. Find his gain/loss percentage?

Ans: 5\displaystyle\frac{5}{19}\% profit

Explanation:

Weight gain = \displaystyle\frac{50}{950}\times 100 = 5\displaystyle\frac{5}{19}\%

Question: A grocery dealer cheats to the extent of 10% while buying as well as selling by using false weight. What is his increase in the profit %?
(a) 20%
(b) 21%
(c) 22%
(d) None of these

Ans: (b) 21%

Explanation:

He has monetary gain of 10% and also weight gain of 10%

Net gain by applying ab method (10, 10) → 10 + 10 + \displaystyle\frac{10\times 10}{100} = 21

Question: A dishonest shopkeeper, using a faulty balance makes a profit of 5% while buying as well as while selling his goods. His actual gain percent in the whole process amounts to
(a) 11
(b) 10
(c) 10.25
(d) 10.5

Ans: (c) 10.25

Explanation:

By applying ab method

(5, 5) → 10 + 0.25 = 10.25

Question: Lalit marks up his goods by 40% and gives a discount of 10%. Apart from this, he uses a faulty balance also, which reads 1000 gm for 800 gm.  What is his net profit percentage?

Ans: 57.5%

Explanation:

Applying ab method,

(MP, discount) → P%

(40, -10) → 30 – 4 = 26%

Weight gain = 25%

Again, applying ab method for overall profit,

(26, 25) → 51 + \displaystyle\frac{26\times 25}{100} = 51 + 6.5 = 57.5%

Question: A shopkeeper wants to make some profit by selling rice. He contemplates about various methods. Which of the following would maximize his profit?
I. Sell rice at 15% profit.
II. Use 850 g of weight instead of 1 kg.
III. Mix 15% impurities in rice and selling rice at cost price.
IV. Increase the price by 7.5% and reduce weights by 7.5%.

(a) I or III
(b) II
(c) II, III and IV
(d) Profits are same

Ans: (b) II

Explanation:

Case-I: Profit % = 15%

Case-II: Faulty weight is used

Weight gain = \displaystyle\frac{\text{Error}}{\text{Faulty weight}}\times 100 = \displaystyle\frac{150}{850}\times 100 = 17.64\%

Case-III: Let, CP of 1kg = Rs. 100

He adds 15% impurities

After adding impurities,

CP of 1 kg = \displaystyle\frac{1150}{100}\times 1000 = 86.95

SP of 1 kg = 100

P% = \displaystyle\frac{13.05}{86.95}\times 100 = 15\%

Case-IV:

\displaystyle\frac{\text{CP}}{\text{SP}} = \displaystyle\frac{9250}{10750}  = \displaystyle\frac{37}{43}

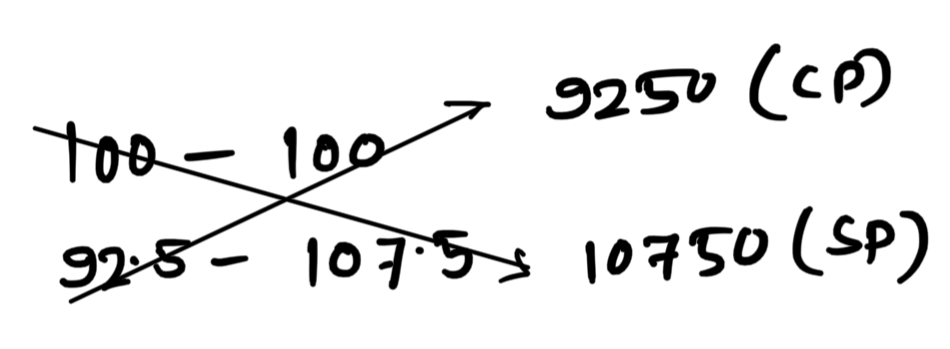
P% = \displaystyle\frac{6}{37}\times 100 = 16.21\%

Now profit summary:
Case-I → 15%
Case-II → 17.64%
Case-III → 15%
Case-IV → 16.21%

So, maximum profit at Case-II

Hence (b) is the correct answer

You may like to read our other post on Profit and Loss from here.

<<Prev

Home

Next>>