Ratio and Proportion - Concepts and Solved Examples

Jump ahead to

What is ratio?

The ratio is a comparison between two quantities of the same unit by division. And one thing to remember that comparison is just not limited to two quantities, quantities can be more than two.

The colon symbol (:) is used as a ratio symbol. Sometimes to indicate ratio slash (/) is also used.

A ratio $a:b$ is to be read as “a is to b“

Say, Arif earns ₹ 70K per month and Jim earns ₹ 60K per month. So the ratio of their earnings will be 70000 : 60000 = 7 : 6. Here we are comparing two earnings with unit ₹.

If, Arif earns $ 70K per month and Jim earns ₹ 60K per month. In this case, you can’t find the ratio directly as the units of the quantities (one is ₹ and another is $) is not identical. But after converting them into the same unit we could do that. If $1 = ₹80 today, required ratio will be $\displaystyle\frac{70000\times 80}{60000}=\displaystyle\frac{280}3{}$ i.e. 280 : 3

But we are not able to find the ratio of Adeel’s weight to salary because they are neither of the same unit nor convertible like the currency of the previous example.

Types of ratio

Based on some operations and properties ratios can be differentiated as follows:

Compound Ratio

The compound ratio is the product of the given ratios.

Question: Find the compound ratio of 2 : 3 and $\displaystyle\frac{4}{5}$

\displaystyle\frac{2}{3}\times \displaystyle\frac{4}{5}=\displaystyle\frac{8}{15}=8:15

Duplicate Ratio

It is the ratio of the squares of the given terms.

Duplicate ratio of $a : b$ ⟶ $a^2 : b^2$

Triplicate Ratio

It is the ratio of the cubes of the given terms.

Duplicate ratio of $a : b$ ⟶ $a^3 : b^3$

Subduplicate Ratio

It is the ratio of the square roots of the given terms.

Subduplicate ratio of $a : b$ ⟶ $\sqrt{a} : \sqrt{b}$

Question: Find the subduplicate ratio of 4 : 9

$4 : 9$ ⟶ $\sqrt{4} : \sqrt{9}=2:3$

Subtriplicate Ratio

It is the ratio of the cube roots of the given terms.

Subtriplicate ratio of $a : b$ ⟶ $\sqrt[3]{a} : \sqrt[3]{b}$

Equivalent Ratio

If two or more ratios in their lowest form are same, the are called equivalent ratio.

30 : 20 and 24 : 16 in lowest form are same as 3 : 2. These are equivalent ratios.

We can get equivalent ratios by multiplying or dividing the numerator and denominator by the same number.

Question: Fill the missing number

$\displaystyle\frac{14}{21}=\displaystyle\frac{?}{3}=\displaystyle\frac{6}{?}$

To get the first missing number, we observe that 21 is divided by 7, so 14 will also be divided by 7.

So the number becomes 2

Hence, second ratio is $\displaystyle\frac{2}{3}$

For second missing term we see that 6 we have got by multiplying by 3 to the numerator of second ratio. So denominator will also be multiplied by 3.

So it becomes 9

Hence, third ratio is $\displaystyle\frac{6}{9}$

So, finally $\displaystyle\frac{14}{21}=\displaystyle\frac{2}{3}=\displaystyle\frac{6}{9}$

Final Ratio

Sometimes $a:b$ and $b:c$ are given and we have to find out $a:b:c$ or the case might be like $a:b$ , $b:c$ and $c:d$ are given and we have to find out $a:b:c:d$ . These are the case of final rato.

How to solve this type of problem?

Case 1 : $a:b$ and $b:c$ ⟶ $a:b:c$

b is the middle term here, so we would make b equal in both ratios by using the LCM of b values from both ratios

Question: If $a : b = 2 : 5$ and $b : c = 4 : 5$ , find out $a : b : c$

b values are 5 and 4

LCM(5, 4) = 20

Now, $a : b = 2 : 5=2\times 4: 5\times 4=8:20$

And $b : c = 4 : 5=4\times 5: 5\times 5=20:25$

Hence, $a: b : c = 8:20:25$

Case 2 : $a:b$ , $b:c$ and $c:d$ ⟶ $a:b:c:d$

First, find out $a:b:c$ with the help of $a:b$ and $b:c$ by equalling b

Second, Find out $a:b:c:d$ with the help of $a:b:c$ and $c:d$ by equalling c

Question: If $a:b=1:2$ , $b:c=3:4$ and $c:d=5:6$ , find out $a:b:c:d$

a:b=1:2=1\times 3:2\times 3=3:6

b:c=3:4=3\times 2:4\times 2=6:8

So, $a:b:c=3:6:8$

Now, $a:b:c=3:6:8=3\times 5:6\times 5:8\times 5=15:30:40$

And, $c:d=5:6=5\times 8:6\times 8=40:48$

Hence, $a:b:c:d=15:30:40:48$

Shortcut to find final ratio

Question: If $a:b=1:2$ , $b:c=3:4$ and $c:d=5:6$ , find out $a:b:c:d$

Let’s try to redo the problem with shortcut

Step 1: Form a matrix like structure as following

Step 2: Fill the blank spaces. Right side blank space of a row will be filled with rightmost digit and left side blank space by the leftmost digit of a row.

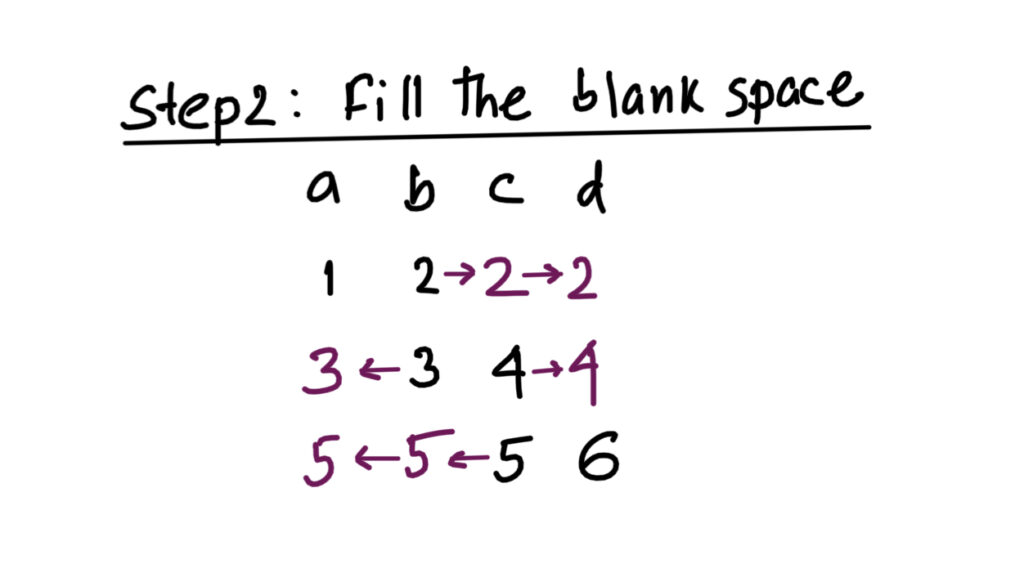
Step 3: Multiply the numbers vertically or column wise and simplify if required to get the final ratio.

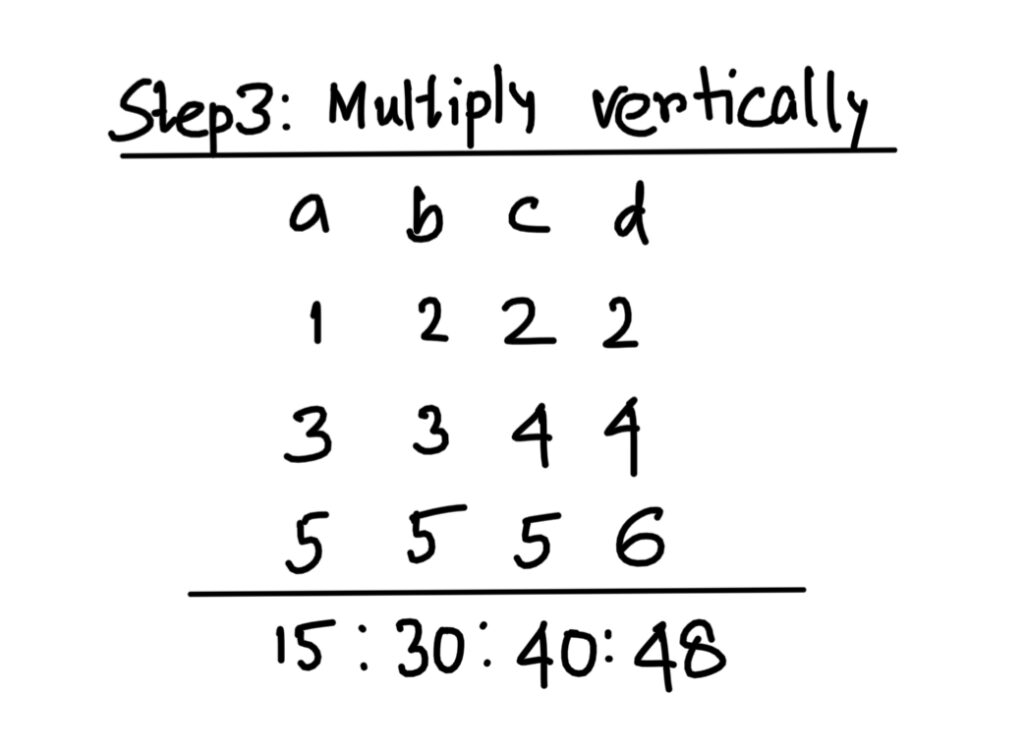
Hence, $a:b:c:d=15:30:40:48$

Question: If $a : b = 2 : 5$ and $b : c = 4 : 5$ , find out $a : b : c$

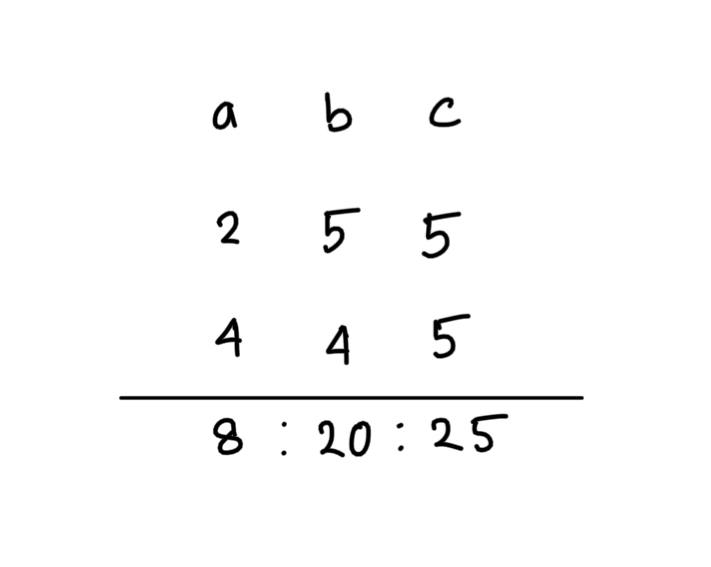
Hence, $a: b : c = 8:20:25$

Question: If $A: B=2:3$ , $B: C=4:5$ and $C: D=6:7$ , what is the value of $A$ , $B$ , $C$ and $D$ ?

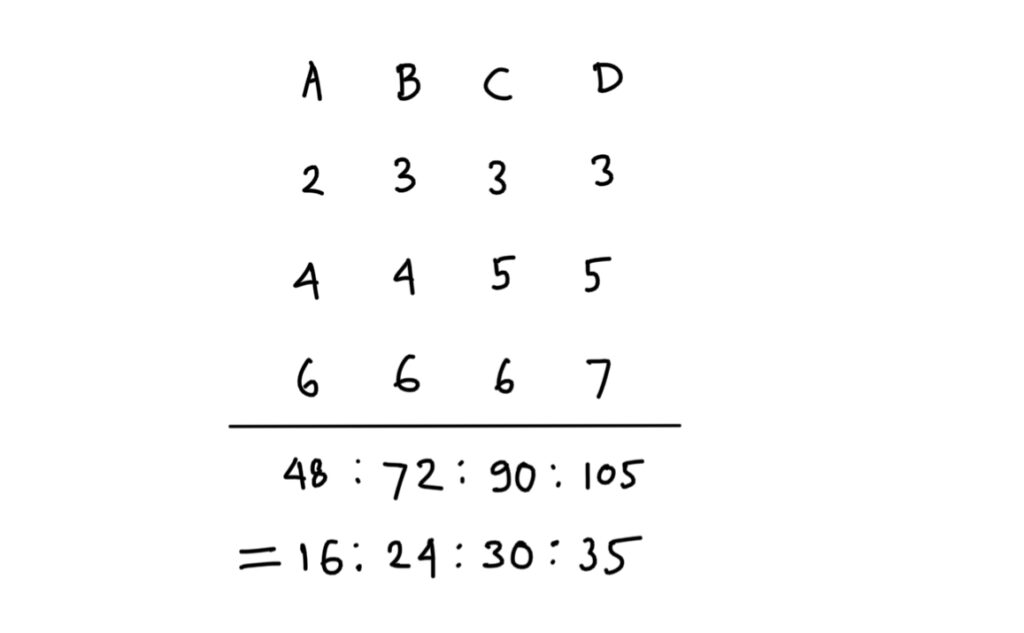
We have got that $A$ , $B$ , $C$ and $D$ are in the ratio of $16:24:30:35$

So, $A = 16x$ , $B = 24x$ , $C = 30x$ , $D = 35x$ , where $x$ can be any number

What is Proportion?

When two ratios are equal the make proportion.

Solved Question Answer

Question: If a : b = 2 : 3, b : c = 4 : 5 and c : d = 6 : 7, then find a : d =
(a) 10 : 21 $\qquad$ (b) 16 : 35 $\qquad$ (c) 44 : 63 $\qquad$ (d) 12 : 35

Ans: (b) 16 : 35

Explanation:

\begin{aligned} &\frac{a}{b}\times \frac{b}{c}\times \frac{c}{d}=\frac{2}{3}\times \frac{4}{5}\times \frac{6}{7}\\[1.5em] &\Rightarrow \frac{a}{d}=\frac{16}{35}\\[1.5em] \end{aligned}

Question: If $\displaystyle\frac{a}{6}=\frac{b}{8}=\frac{c}{12}$ , then fin a : b : c

(a) 4 : 1 : 2 $\qquad$ (b) 1 : 3 : 2 $\qquad$ (c) 3 : 6 : 4 $\qquad$ (d) 3 : 4 : 6

Ans: (d) 3 : 4 : 6

Explanation:

a : b : c = 6 : 8 : 12 = 3 : 4 : 6

Question: If (3x + 4y) : (4x – 3y) = 5 : 3, find x : y
(a) 27 : 11 $\qquad$ (b) 12 : 29 $\qquad$ (c) 29 : 12 $\qquad$ (d) 17 : 9

Ans: (a) 27 : 11

Explanation:

\begin{aligned} & \frac{3x+4y}{4x-3y}=\frac{5}{3}\\ & \Rightarrow 5(4x-3y)=3(3x+4y)\\ & \Rightarrow 20x-15y=9x+12y\\ & \Rightarrow 11x=27y\\ & \Rightarrow \frac{x}{y}=\frac{27}{11}\\ & \Rightarrow x:y=27:11 \end{aligned}

Question: If $a:b=2:3$ , find $\displaystyle \frac{3a^3+4b^2a}{5a^2b+5b^3}$

(a) 7 : 10 $\qquad$ (b) 32 : 65 $\qquad$ (c) 15 : 41 $\qquad$ (d) 19 : 63

Ans and Explan a tion

Question: The present age of P and Q are in the ratio of 2 : 3. After 3 years from now ratio of their ages will become 9 : 13. What would have been their ratio of their ages 4 years ago?
(a) 5 : 7 $\qquad$ (b) 5 : 8 $\qquad$ (c) 4 : 7 $\qquad$ (d) 7 : 5

Ans: (b) 5 : 8

Explanation:

Present age

P = 2x
Q= 3x

Now,

\begin{aligned} &\quad \frac{2x+3}{3x+3}=\frac{9}{13}\\[1em] &\Rightarrow 27x+27=26x+39\\ &\Rightarrow x=12 \end{aligned}

Ratio of ages 4 years ago
= $\displaystyle \frac{2x-4}{3x-4}$

= $\displaystyle \frac{20}{32}$

= $\displaystyle \frac{5}{8}$

Question: Instead of dividing Rs. 133 among A, B and C in the ratio $\displaystyle \frac{1}{2} : \displaystyle\frac{1}{4} : \displaystyle\frac{1}{6}$ , by mistake it was divided in the ratio of $2:4:6$ . Who gained in the transaction?
(a) Only A $\qquad$ (b) Only B $\qquad$ (c) Only C $\qquad$ (d) Both B and C

Ans and Explanation

Question: The ratio of expenditure of Ram and Shyam is 5 : 8. If the expenditure of Ram is increased by 25% and the expenditure of Shyam is decreased by 25%, then what be the ratio of their new expenditure?
(a) 25 : 24 $\qquad$ (b) 24 : 25 $\qquad$ (c) 21 : 23 $\qquad$ (d) 23 : 21

Ans: (a) 25 : 24

Explanation:

Let, expenditure of Ram = R
and expenditure of Shyam = S

\displaystyle\frac{\text{R}}{\text{S}}=\displaystyle\frac{5}{8}

New,

\begin{aligned} \frac{\text{R}}{\text{S}}&=\frac{5\times 125\%}{8\times 75\%}\\[1.5em] &=\frac{5\times 125}{8\times 75}\\[1.5em] &=\frac{25}{24}\\ \end{aligned}

Question: The monthly income of A and B are in the ratio of 4 : 5 and their monthly expenses are in the ratio of 8 : 11. If each of them saves Rs. 1600 per month, then monthly income of B is
(a) Rs. 2500 $\qquad$ (b) Rs. 6000 $\qquad$ (c) Rs. 3500 $\qquad$ (d) Rs. 4000

Ans and Explanation

Question: Two positive numbers are in the ratio of 3 : 4. The difference between the squares is 63. Find the bigger number.
(a) 16 $\qquad$ (b) 10 $\qquad$ (c) 8 $\qquad$ (d) 12

Ans: (d) 12

Explanation:

Let, the number are 3x, 4x

$\Rightarrow$ (4x)² – (3x)² = 63

$\Rightarrow$ 16x² – 9x² = 63

$\Rightarrow$ 7x² = 63

$\Rightarrow$ x = 3

So, bigger number = 4x = 12

Question: What must be added to each term of the ratio 9 : 17 so that the ratio become 3 : 4?
(a) 9 $\qquad$ (b) 15 $\qquad$ (c) 6 $\qquad$ (d) 18

Ans: (b) 15

Explanation:

Let, x is to be added

\begin{aligned} &\quad \frac{9+x}{17+x} = \frac{3}{4}\\[1.5em] &\Rightarrow 36+4x=51+3x\\[1.5em] &\Rightarrow x= 15 \end{aligned}

Question: Find the duplicate ratio of $2\sqrt{2} : 3\sqrt{2}$
(a) 2 : 3 $\qquad$ (b) 3 : 2 $\qquad$ (c) 4 : 9 $\qquad$ (d) 3 : 4

Ans: (c) 4 : 9

Explanation:

\begin{aligned} \text{Duplicate Ratio} & = (2\sqrt{2})^2 : (3\sqrt{2})^2\\ &= 2^2 : 3^2\\ &=4:9 \end{aligned}

Question: Find the sub-duplicate ratio of 64 : 121
(a) 8 : 13 $\qquad$ (b) 4 : 5 $\qquad$ (c) 8 : 9 $\qquad$ (d) 8 : 11

Ans: (d) 8 : 11

Explanation:

\begin{aligned} \text{Sub-duplicate Ratio} & = \sqrt{64} : \sqrt{121}\\ &= 8 : 11\\ \end{aligned}

Question: Find the sub triplicate ratio of $\sqrt{64} : \sqrt{729}$
(a) 8 : 27 $\qquad$ (b) 3 : 2 $\qquad$ (c) 27 : 8 $\qquad$ (d) 2 : 3

Ans: (d) 2 : 3

Explanation:

\sqrt{64} : \sqrt{729}=8:27

\begin{aligned} \text{Sub triplicate Ratio} & = \sqrt[3]{8} : \sqrt[3]{27}\\ &= 2 : 3\\ \end{aligned}

Question: Two numbers A and B are in the ratio of 4 : 5. Their average is 180. If A is increased by 20% then to get the average increased by , B will increase by
(a) 40 $\qquad$ (b) 50 $\qquad$ (c) 60 $\qquad$ (d) 70

Ans and Explanation

Join Us

Join the discussion and ask any question of maths and reasoning directly to us and other like-minded user just like you!

👉 More on Mathematics for Competitive Exam

<<Prev

Home

Next>>

Please share this post with someone who might find it helpful.

Ratio and Proportion – Concepts and Solved Examples

What is ratio?