The annual earning of Mr. Sikkawala is Rs. 4 lakhs per annum for the first year of his job and his expenditure was 50%. Later on for the next 3 years his average income increases by Rs.40,000 per annum and the saving was 40%, 30% and 20% of the income. What is the percentage of his total savings over the total expenditure if there is no interest is applied on the savings for these four years?
(a) 49%
(b) 37%
(c) 87%
(d) 51%

Ans: (d) 51%

Explanation:

Increment in salary = \displaystyle\frac{40k}{400k}\times 100 = 10%

Let, initial salary = 100

Year	Salary	Savings %	Savings
1	100	50%	50
2	110	40%	44
3	120	30%	36
4	130	20%	26

For 4 years,
Total salary = 100 + 110 +120 +130 +140 = 460
Total savings = 50 + 44 +36 + 26 = 156

∴ Total expenditure = 460 – 156 = 304

Now, \displaystyle\frac{\text{Savings}}{\text{Expenditure}}\times 100 = \displaystyle\frac{156}{304}\times 100 = 51%

Note: To get the answer we could use approximation. Denominator is slightly less than twice numerator. So, answer will be slightly more than 50%. From option we could choose 51% as the answer.

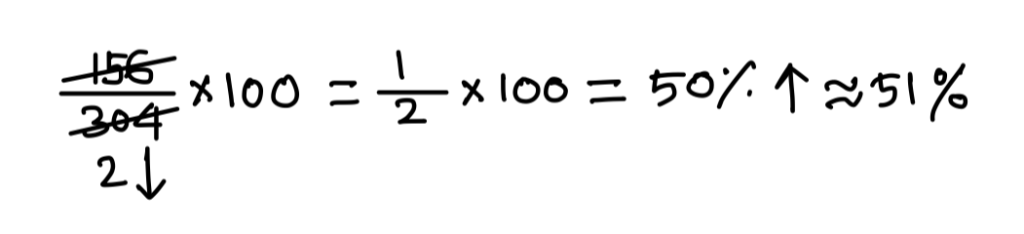
If you do the real calculation,

\displaystyle\frac{156}{304}\times 100 = 51.3157% ≈ 51%