Average Advanced Problems

<<Prev

Home

Next>>

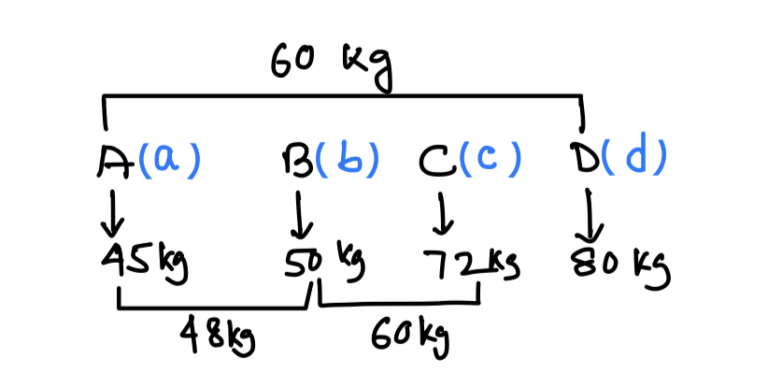
Question: The average weight of the students in four sections A, B, C and D is 60 kg. The average weight of the students of A, B, C and D individually are 45 kg, 50 kg, 72 kg and 80 kg respectively. If the average weight of the students of A and B together is 48 kg and that of B and C together is 60 kg, what is the ratio of the number of students in sections A and D?
(a) 12 : 7
(b) 4 : 3
(c) 3 : 2
(d) 8 : 5

Ans: (b) 4 : 3

Explanation:

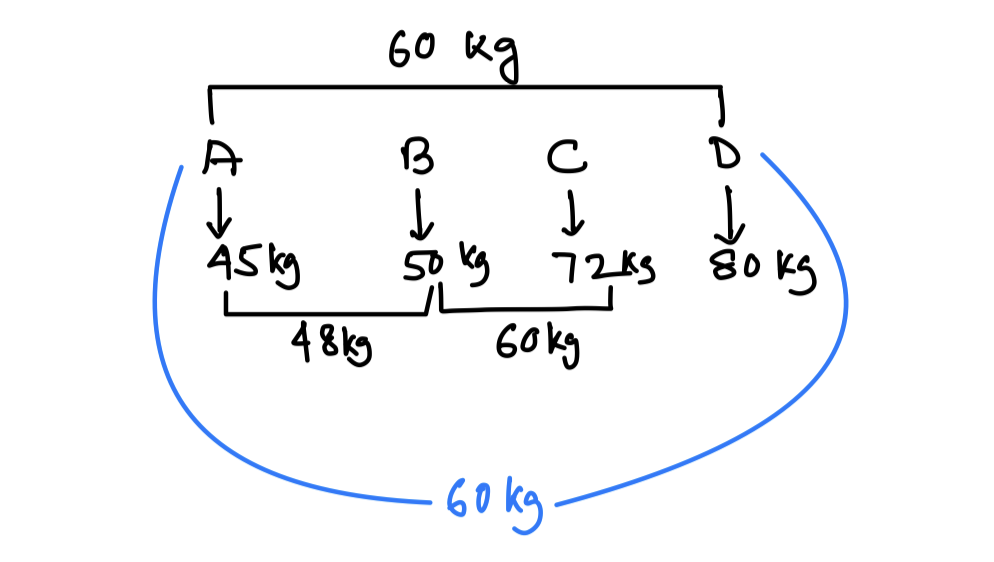
Avg of B and C is 60.
When avg of A and D is also considered there is no change in overall avg of 60 kg
Hence avg of A and D is also 60

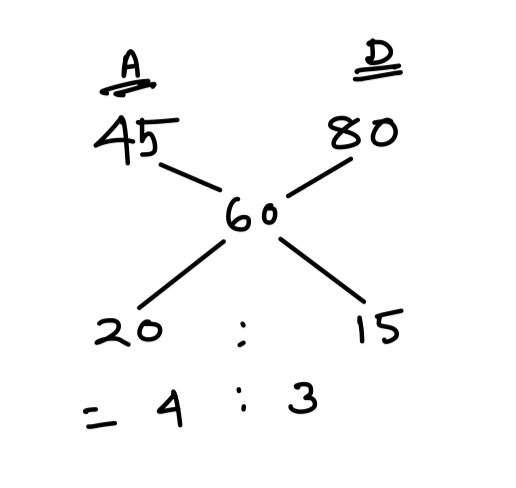
Aliter 1(By Applying Alligation)

Let, no of students in section A, B, C and D are a, b, c and d respectively.

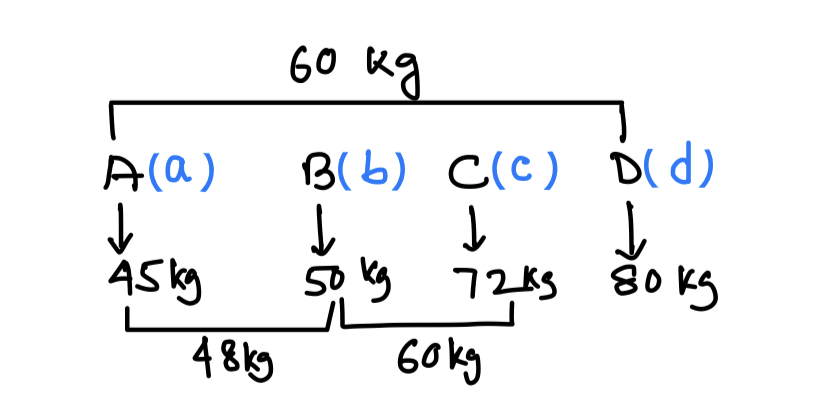
a : b = 2 : 3
b : c = 12 : 10 = 6 : 5

∴ a : b : c = 4 : 6 : 5

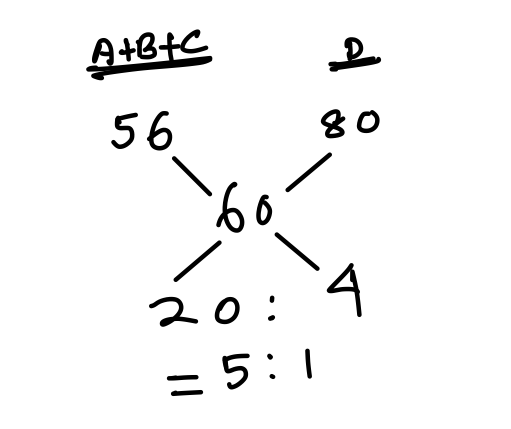
If d = 1, a + b + c = 5
We know, a : b : c = 4 : 6 : 5

∴ a = \displaystyle\frac{4}{15}\times 5 = \displaystyle\frac{4}{3}

∴ a : d = \displaystyle\frac{4}{3} : 1 = 4 : 3

Aliter 2 (By traditional Method)

Let, no of students in section A, B, C and D are a, b, c and d respectively.

Finally, 45a + 50b + 72c + 80d = 60(a + b + c + d)
⇒ 45a + 50b + 72c + 80d = 60a + 60b + 60c + 60d
⇒ 15a + 10b – 12c = 20d
⇒ 15a + 10 ∙ \displaystyle\frac{3}{2}a – 12 ∙ \displaystyle\frac{5}{4}a = 20d
⇒ 15a + 15a – 15a = 20d
⇒ \displaystyle\frac{\text{a}}{\text{d}} = \displaystyle\frac{20}{15} = \displaystyle\frac{4}{3}

Note: The first method is very much this problem specific whereas Aliter 1 and Aliter 2 is general method. Between Aliter 1 and Aliter 2 we would go with Aliter 1 i.e alligation method since it is more easy to apply. See the next problem.

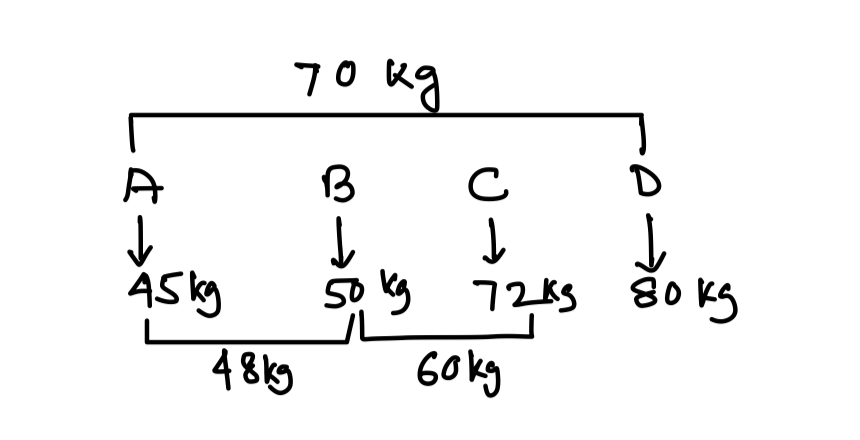
Question: The average weight of the students in four sections A, B, C and D is 70 kg. The average weight of the students of A, B, C and D individually are 45 kg, 50 kg, 72 kg and 80 kg respectively. If the average weight of the students of A and B together is 48 kg and that of B and C together is 60 kg, what is the ratio of the number of students in sections A, B, C and D?
(a) 4 : 6 : 5 : 7
(b) 4 : 6 : 5 : 14
(c) 4 : 6 : 5 : 21
(d) 4 : 6 : 5 : 28

Ans: (c) 4 : 6 : 5 : 21

Explanation:

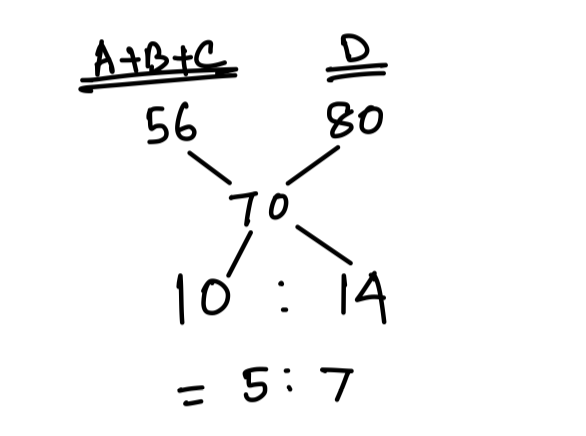
n_A : n_B = 2 : 3
n_B : n_C = 12 : 10 = 6 : 5

\therefore n_A : n_B : n_C = 4 : 6 : 5

If n_D = 7, n_A + n_B + n_C = 5
We know, n_A : n_B : n_C = 4 : 6 : 5

\therefore n_A = \displaystyle\frac{4}{15}\times 5 = \displaystyle\frac{4}{3}

n_B = \displaystyle\frac{6}{3};

n_C = \displaystyle\frac{5}{3};

and n_D = 7 = \displaystyle\frac{21}{3}

\therefore n_A : n_B : n_C : n_D = 4 : 6 : 5 : 21

Question: The average run per wicket of a bowler is 24.85. In the next match he gives 52 runs and takes 5 wickets and average improves by 0.85. Find the total number of wickets he has taken?
(a) 80
(b) 85
(c) 75
(d) 90

Ans: (b) 85

Explanation:

If we read the question carefully we would understand what formula we have to take.

It is given that, “The average run per wicket of a bowler is 24.85″

\text{Bowling avg} = \displaystyle\frac{\text{Runs given}}{\text{Wickets taken}}

Let, bowling avg is 24.85 when wickets taken is x.
In this situation runs given = 24.85x

When 5 more wickets is taken by giving 52 runs, avg is improved by 0.85

Hence, improved avg = 24.85 -0.85 = 24
Note: bowling avg is improved if less runs are given whereas batting avg is improved if more runs are taken

∴ 24.85x + 52 = 24(x + 5)
⇒ 24.85x + 52 = 24x + 120
⇒ 0.85x = 68
⇒ x = 80

Total wickets taken = x + 5 = 85

Question: The average of 4 distinct prime numbers a, b, c, d is 35, where a < b < c < d. a and d are equidistant from 36; b and c are equidistant from 34; a and b are equidistant from 30; and c and d are equidistant from 40. The difference between a and d is:
(a) 30
(b) 14
(c) 21
(d) Can’t be determined

Ans: (b) 14

Explanation:

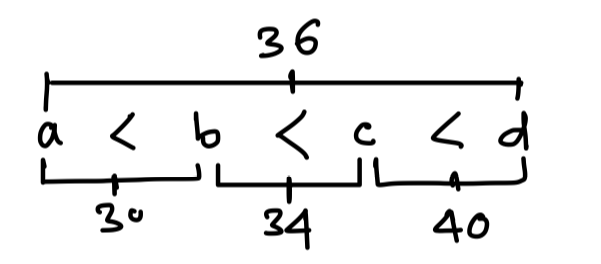
Avg of a and b is 30
And a < 30 < b
And immediate less prime number than 30 is 29

Hence, a + b = 2 × 30 = 60
⇒ b = 60 – 31

OR, the above calculation can be done orally if we think this way
30 – a = 30 – 29 = 1
b will be 1 more than avg = 30 + 1 = 31

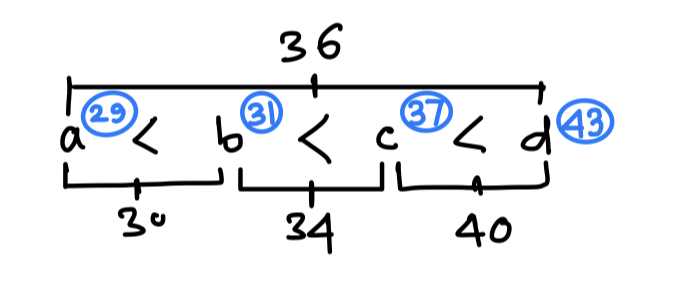
Now, if we find avg of a and d, it comes as \displaystyle\frac{29+43}{2} = \displaystyle\frac{72}{2} = 36 which is our given value, so our initial guess was absolutely correct

∴ d – a = 43 – 29 = 14

Question. The average of 26, 29, n, 35 and 43 lies between 25 and 35. If n is always an integer and greater than average of the given integers, then the value of n is:
(a) 33 < n < 41
(b) 34 < n < 42
(c) 33 < n < 42
(d) None of these.

Ans: (c) 33 < n < 42

Explanation:

Nos are 26, 29, n, 35, 43
Sum = 26 + 29 + n + 35 + 43 = 133 + n

Avg = \displaystyle\frac{133+n}{5}

Given that, 25 < avg < 35

Avg of given integers = \displaystyle\frac{133}{4} = 33.25

n_min = 34

Using inequality, n > 33

Now, let’s combine all three inequalities

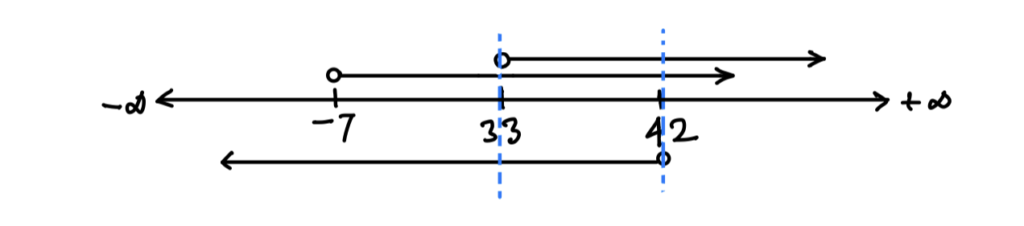
we have the area where all inequalities overlap
33 < n < 42

Question. In an exam of 100 marks, the average marks of a class of 40 students is 76. If the top 3 scorers of the class leave, the average score falls down by 1. If the other two toppers except the highest topper scored not more than 85 marks, then what is the minimum score did topper can score?
(a) 88
(b) 98
(c) 95
(d) 92

Ans: (c) 95

Explanation:

Marks obtained by the top 3 scorers
= 76 × 3 + 1 × 37
= 228 + 37
= 265

Score by the next two toppers ≤ 85

Maximum score they could have = 85 + 85 = 170

Hence minimum score by topper = 265 – 170 = 95

Question. Average score of 52 students of a class is 85. If top five scorer are excluded then the average is decreased by 2. All five scorer are distinct integer and none of them is less than 80. 4 scorers out of 5 form an arithmetic progression having common difference 2. Find the maximum possible score of the topper.
(a) 177
(b) 187
(c) 199
(d) None of these

Ans: (b) 187

Explanation:

Score by 5 toppers
= 5 × 85 + 2 × 47
= 425 + 94
= 519

Score by the all toppers ≥ 80

Topper scores max when rest of the toppers score their min

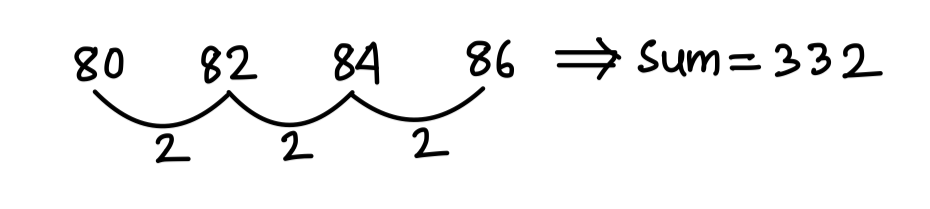
Scores by next 4 toppers = 80 + 82 +84 + 86 = 332

Hence, score by topper = 519 – 332 = 187

Question. The average score in an examination taken by 52 students of a class is 85. If the score of the top five performers excluded, the average scores of the students falls by 2. If none of the top five performer score below 80 and if each of them had distinct integral scores, find the maximum possible scores of the topper.
(a) 187
(b) 199
(c) 177
(d) 193

Ans: (d) 193

Explanation:

Score by top 5 performers
= 5 × 85 + 2 × 47
= 425 + 94
= 519

Score by the all top performers ≥ 80

Top performer scores max when rest of the top performers score their min

Scores by next 4 top performers = 80 + 81 +82 + 83 = 326

Hence, score by topper = 519 – 326 = 193

Question. The average weight of a group of 6 people is decreased by 2 kg when a person weighing 90 kg is replaced by a new person. If this new person is again replaced by another person weighing 30 kg less than the new person. What is the total change in the average weight of the group?
(a) 5
(b) 7
(c) 8
(d) 9

Ans: (b) 7

Explanation:

Change in weight = – 2 × 6 – 30 = – 42

Change in avg = \displaystyle\frac{-42}{6} = -7

Avg will decrease by 7kg

Aliter

Weight of new person = 90 – 2 × 6 = 78
Wight of another person = 78 – 30 = 48

Decrease in weight due to 2nd person = 78 – 48 = 30

Decrease in avg due to 2nd person = \displaystyle\frac{30}{6} = 5 kg

We already know, decrease in avg due to 1st person = 2 kg

Hence, total decrease in avg = (5 + 2) kg = 7 kg

<<Prev

Home

Next>>